2015-01-21
1231
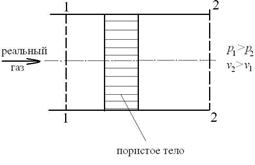
Эффект Джоуля-Томсона – это явление изменения температуры газа при адиабатном дросселировании, когда происходит расширение газа без совершения внешней работы и без теплообмена за счет преодоления гидравлического сопротивления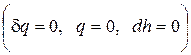 
. При этом затрачивается работа проталкивания 
:
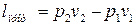Получим дифференциальное уравнение эффекта Джоуля-Томсона. Для этого запишем функцию состояния - энтальпию в виде: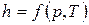 
.
Ее дифференциал – полный дифференциал, равный:
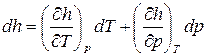. (1)
Удельная теплоемкость при p =const по определению равна:
. (2)
Производную 
, входящую в (1), получим из объединенного выражения 1-го и 2-го законов термодинамики:
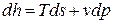. (3)
Разделим уравнение (3) на величину dp при Т =const. Тогда получим уравнение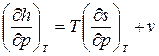 
, в котором заменим 
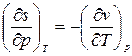, используя уравнения Максвелла (дифференциальные соотношения взаимности). Тогда получим:
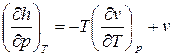. (4)
Подставим в уравнение (1) значения производных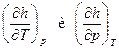 
из выражений (2) и (4), учитывая, что dh =0:
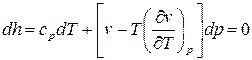, (5)
или при h =const:
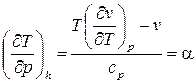. (6)
Уравнение (6) является дифференциальным уравнением эффекта Джоуля-Томсона, которое позволяет определить характер изменения температуры в процессе дросселирования. В уравнении (6) величина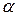 
называется дифференциальным температурным коэффициентом дросселирования. Для определения величины 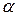требуется знать термическое уравнение состояния и теплоемкость ср для данного вещества.
Поскольку величина dp отрицательна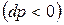 
, то знак величины dT в уравнении (6) противоположен знаку числителя этого уравнения. Для идеального газа термическое уравнение состояния: pv=RT. Тогда производная 
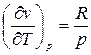и числитель уравнения (6) равен 
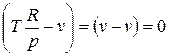, т.е. коэффициент 
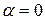. Для реальных газов и паров возможны три случая в зависимости от начального состояния газа перед дросселированием:
1. 
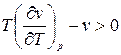. Тогда 
;
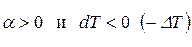2. 
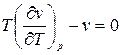. Тогда 
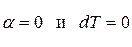- уравнение инверсии;
3. 
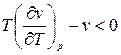. Тогда 
.
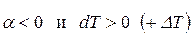Точка, в которой dT =0, есть точка инверсии (перестановки). Температура Т 2= Т 1= Тинв – температура инверсии. В критической точке для всех веществ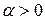 
и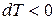 
, т.е. реализуется 1-ый случай. Проиллюстрируем эти случаи дросселирования с помощью паровой диаграммы T-v для изобары (p =const):
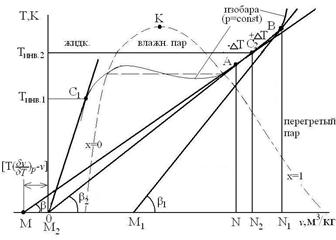
где х – степень сухости пара; tg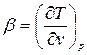 
.
1-ый случай: Если начальное состояние вещества перед дросселированием определяется точкой А, то отрезок на графике MN=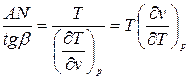 
является первым слагаемым числителя выражения (6), а отрезок М О =MN- O N= 
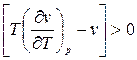является числителем выражения (6), так как MN>ON.
Таким образом, для этого случая и 
, т.е. газ при дросселировании охлаждается.
2-ой случай: Если начальное состояние перед дросселированием определяется точкой В, то отрезок M1N1< O N1 и М1 О =M1N1- O N1 
.
Тогда, согласно уравнению (6), 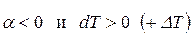и газ при дросселировании нагревается.
3-ий случай: Если начальное состояние вещества перед дросселированием определяется точками С 1 и С 2,то отрезок М 20=0 и согласно уравнению (6),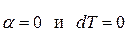 
, т.е. температура газа не изменяется при дросселировании (точка М 2 совпадает с началом координат). Точки С 1 и С 2 – точки инверсии. Для любой изобары реального газа имеются две точки инверсии С 1 и С 2, где С 1 – в области жидкости и С 2 – в области перегретого пара.
Реальный газ или пар можно путем дросселирования перевести в жидкое состояние в том случае, если его начальная температура перед дросселированием будет меньше температуры инверсии Тинв 2. Положительный эффект Джоуля-Томсона используется в холодильной технике для получения холода.
