1. 
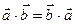 — переместительный закон.
— переместительный закон.
2. 
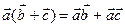 — распределительный закон.
— распределительный закон.
3.  Если
Если 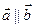 то
то 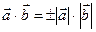 .
.
4. 
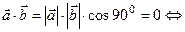
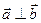 (или
(или 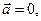 или
или 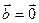 ).
).
В частности, скалярное произведение единичных векторов (ортов) удовлетворяет равенствам:
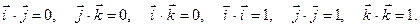

5.  Если векторы заданы координатами
Если векторы заданы координатами  ,
, 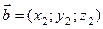 или
или 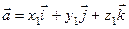 ,
, 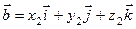 , то
, то

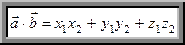 .
.
6.  Угол между векторами
Угол между векторами 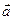 и
и 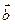 определяется по формуле:
определяется по формуле:

 .
. 
7.  Векторы
Векторы 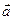 и
и 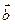 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.:
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.:
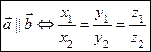 .
.
8.  Условие перпендикулярности векторов
Условие перпендикулярности векторов 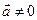 и
и 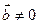 :
:
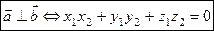 .
.
Пример 3.4. Векторы 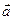 и
и 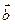 образуют угол
образуют угол 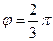 . Зная, что
. Зная, что 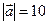 и
и 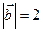 , вычислите
, вычислите  .
.

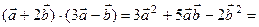
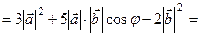
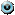
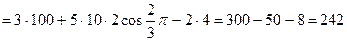 .
.
 Пример 3.5. Даны вершины треугольника
Пример 3.5. Даны вершины треугольника  ,
, 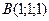 и
и 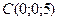 . Найдите: 1) внутренний угол при вершине
. Найдите: 1) внутренний угол при вершине 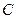 ;
;
2) 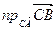 .
.
 Для нахождения угла
Для нахождения угла 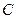 найдём векторы
найдём векторы 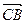 и
и  .
.
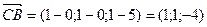 ;
;
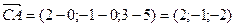 .
.
Тогда 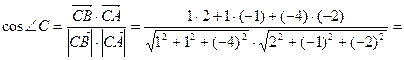

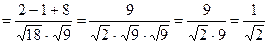 Т.е.
Т.е. 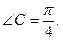
Согласно формуле (*)

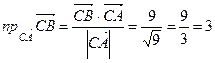 .
.
 2015-01-21
2015-01-21 1012
1012








