 |
Под углом между прямыми на плоскости понимают наименьший (острый) из двух смежных углов, образованных этими прямыми.
 Если прямые
Если прямые 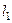 и
и 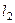 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 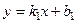 и
и 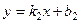 , то
, то
v угол 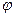 между ними вычисляется с помощью формулы
между ними вычисляется с помощью формулы
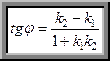 (8)
(8)
v условие параллельности прямых 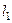 и
и 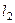 имеет вид
имеет вид
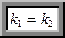 (9)
(9)
v условие перпендикулярности прямых 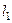 и
и 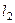 имеет вид
имеет вид
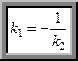 (10)
(10)
 Если прямые
Если прямые 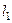 и
и 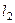 заданы общими уравнениями
заданы общими уравнениями 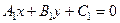 и
и 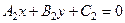 , то
, то
v угол 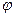 между ними вычисляется с помощью формулы
между ними вычисляется с помощью формулы
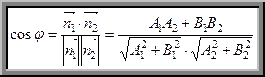 , (11)
, (11)
где 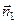 и
и 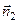 — нормальные векторы прямых
— нормальные векторы прямых 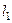 и
и 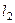 .
.
v условие параллельности прямых 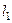 и
и 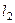 имеет вид
имеет вид
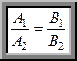 (12)
(12)
Это условие вытекает из того, что если прямые 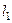 и
и 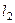 параллельны, то их нормальные векторы
параллельны, то их нормальные векторы 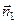 и
и 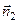 коллинеарны, а это значит, что их соответствующие координаты пропорциональны.
коллинеарны, а это значит, что их соответствующие координаты пропорциональны.
v условие перпендикулярности прямых 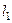 и
и 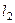 имеет вид
имеет вид
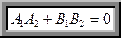 (13)
(13)
Это условие вытекает из того, что если прямые 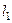 и
и 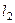 перпендикулярны, то и их нормальные векторы
перпендикулярны, то и их нормальные векторы 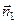 и
и 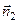 тоже перпендикулярны, а это значит, что скалярное произведение этих векторов равно нулю.
тоже перпендикулярны, а это значит, что скалярное произведение этих векторов равно нулю.
Пример4.4. Вычислите угол между прямыми
а) 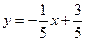 и
и 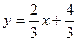 ;
;
б) 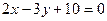 и
и 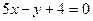 ;
;
в) 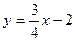 и
и 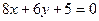 .
.
 а) Воспользуемся формулой (8). Подставляя в неё значения
а) Воспользуемся формулой (8). Подставляя в неё значения 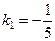 и
и 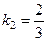 , находим
, находим
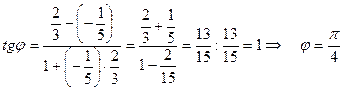 .
.
Ответ: 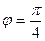 .
.
б) Подставим значения 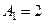 ,
, 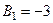 ,
, 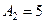 ,
, 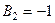 в формулу (11):
в формулу (11):
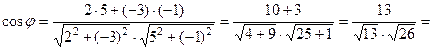
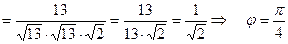 .
.
Ответ: 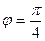 .
.
в) Здесь 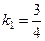 , найдём
, найдём 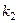 .
.
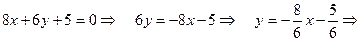
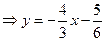 . Тогда
. Тогда 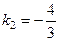 .
.
Так как 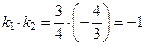 , то данные прямые перпендикулярны. (По формуле (8) получаем:
, то данные прямые перпендикулярны. (По формуле (8) получаем: 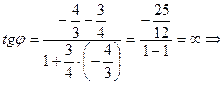
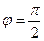 ).
).
 Ответ:
Ответ: 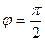 .
.

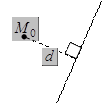 Расстоянием
Расстоянием 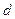 от точки
от точки 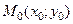 до прямой
до прямой 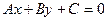 называется длина перпендикуляра, опущенного из этой точки на прямую и вычисляется по формуле:
называется длина перпендикуляра, опущенного из этой точки на прямую и вычисляется по формуле:

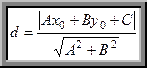 (14)
(14)
Пример 4.5. Найдите расстояние от точки 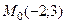 до прямой
до прямой 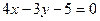 .
.
 Подставляя в формулу (14) данные задачи, получим
Подставляя в формулу (14) данные задачи, получим

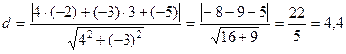 .
.
Ответ: 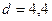 лин. ед.
лин. ед.

 2015-01-21
2015-01-21 871
871








