 |
 Если каждому числу
Если каждому числу 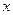 из некоторого множества
из некоторого множества 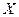 соответствует одно и только одно число
соответствует одно и только одно число 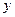 , то говорят, что на множестве
, то говорят, что на множестве 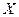 задана функция.
задана функция.
Переменная 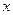 при этом называется независимой переменной (или аргументом), а переменная
при этом называется независимой переменной (или аргументом), а переменная 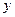 — зависимой.
— зависимой.
 Способ (правило), с помощью которого устанавливается соответствие, определяющее данную функцию, обозначают той или иной буквой:
Способ (правило), с помощью которого устанавливается соответствие, определяющее данную функцию, обозначают той или иной буквой: 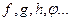 . Т.е. то обстоятельство, что
. Т.е. то обстоятельство, что 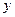 есть функция аргумента
есть функция аргумента 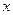 , кратко выражают записью:
, кратко выражают записью: 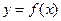 или
или 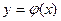 и т.п.
и т.п.
Множество 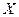 называется областью определения функции и обозначается
называется областью определения функции и обозначается 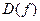 , а множество всех чисел
, а множество всех чисел 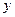 , соответствующих различным числам
, соответствующих различным числам 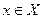 — областью значений этой функции и обозначается
— областью значений этой функции и обозначается 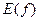 .
.
Эти области могут представлять собою отдельные точки числовой прямой, отрезки, интервалы этой прямой, множество всех действительных чисел.
 Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
 Пусть заданы прямоугольная система координат
Пусть заданы прямоугольная система координат 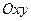 и функция
и функция 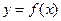 .
.
Графиком функции 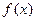 называют множество всех точек плоскости с координатами
называют множество всех точек плоскости с координатами 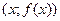 , где
, где 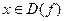 .
.
Для функции, заданной аналитически, т.е. уравнением 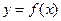 , под графиком понимают множество точек
, под графиком понимают множество точек 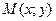 плоскости, координаты которых удовлетворяют уравнению
плоскости, координаты которых удовлетворяют уравнению 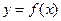 .
.
График функции есть некоторая линия на плоскости. Например, уравнение 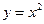 задаёт функцию, графиком которой является парабола.
задаёт функцию, графиком которой является парабола.
Функция, заданная аналитически уравнением 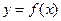 , определена в точке
, определена в точке 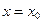 , если возможно вычислить
, если возможно вычислить 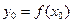 . Множество таких точек образует область определения функции.
. Множество таких точек образует область определения функции.
Пример 6.1. Найдите область определения функции:
а) 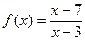 ; б)
; б) 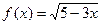 ; в)
; в) 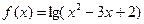 .
.
 а) Дробь
а) Дробь 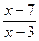 определена, если её знаменатель не равен нулю. Область определения данной функции можно найти из условия
определена, если её знаменатель не равен нулю. Область определения данной функции можно найти из условия 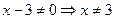 . Таким образом,
. Таким образом, 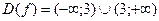 .
.
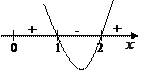 б) Функция
б) Функция 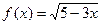 определена, если подкоренное выражение неотрицательно, т.е.
определена, если подкоренное выражение неотрицательно, т.е. 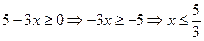 . Значит,
. Значит, 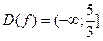 .
.
в) Логарифм определён, когда

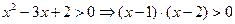 .
.
Значит, 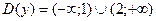 .
.
 Основными (или простейшими) элементарными функциями называются:
Основными (или простейшими) элементарными функциями называются:
| постоянная функция | 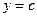 ; ;
|
| степенная функция | 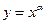 , , 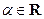 ; ;
|
| показательная функция | 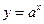 , , 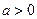 ; ;
|
| логарифмическая функция | 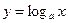 , , 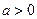 , , 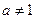 ; ;
|
| тригонометрические функции | 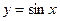 ; ; 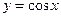 ; ;
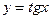 ; ; 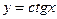 ; ;
|
| обратные тригонометрические функции | 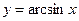 ; ; 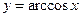 ; ;
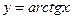 ; ; 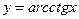 . .
|
 Функция, аргумент которой в свою очередь есть функция (
Функция, аргумент которой в свою очередь есть функция (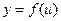 , где
, где 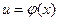 ), называется сложной функцией (или композицией функций).
), называется сложной функцией (или композицией функций).
Пример 6.2. Функция 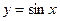 — простейшая,
— простейшая,
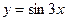 — сложная
— сложная
(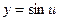 ,
, 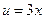 ).
).
Пример 6.3. Функция 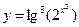 сложная, которая может быть представлена следующей цепью основных элементарных функций:
сложная, которая может быть представлена следующей цепью основных элементарных функций: 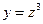 ,
, 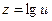 ,
, 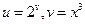 .
.
 |
Элементарными функциями называются функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (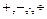 ) и композиций (т.е. образования сложных функций). Все остальные функции называются неэлементарными.
) и композиций (т.е. образования сложных функций). Все остальные функции называются неэлементарными.
Пример 6.4. Примером неэлементарной функции может служить функция вида: 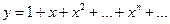
Формула 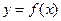 определяет явный способ задания функции. Однако во многих случаях приходится использовать неявный способ задания функции.
определяет явный способ задания функции. Однако во многих случаях приходится использовать неявный способ задания функции.
 |
Неявной называют функцию, которая задана уравнением вида 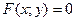 , неразрешенным относительно функции
, неразрешенным относительно функции 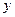 .
.
Пример 6.5. Уравнение 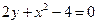 задает неявно функцию
задает неявно функцию 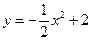 .
.
Пусть для любых различных значений 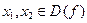 справедливо, что
справедливо, что 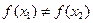 . Тогда для любого
. Тогда для любого 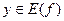 найдётся только одно значение
найдётся только одно значение 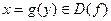 , такое, что
, такое, что 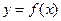 .
.
 |
Функция 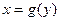 , определённая на
, определённая на 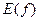 , называется обратной для функции
, называется обратной для функции 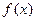 .
.
Пример 6.6. Найдите обратную функцию для данной:
а) 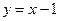 ; б)
; б) 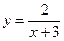 ; в)
; в) 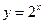 .
.
 а) Для функции
а) Для функции 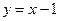 обратной функцией является функция
обратной функцией является функция 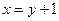 , или в стандартной форме
, или в стандартной форме 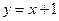 .
.
б) Разрешим уравнение 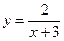 относительно
относительно 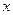 :
: 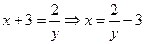 . Обратной функцией является функция
. Обратной функцией является функция 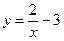 .
.
 в) Для функции
в) Для функции 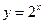 обратной функцией является функция
обратной функцией является функция 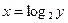 , или в стандартной форме
, или в стандартной форме 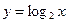 .
.
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.

 2015-01-21
2015-01-21 446
446








