1. Уравнением 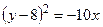 задается парабола, ветви которой направлены:
задается парабола, ветви которой направлены:
а) вверх; б) вниз; в) вправо; г) влево.
2. Каноническое уравнение гиперболы с мнимой полуосью 3 имеет вид:
а) 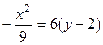 ; б)
; б) 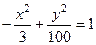 ; в)
; в) 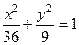 ;
;
г) 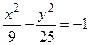 .
.
3. Уравнение 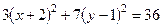 задает:
задает:
а) эллипс; б) гиперболу; в) окружность; г) параболу.
4. Уравнение параболы с вершиной в точке 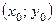 и осью симметрии, параллельной оси OY, имеет вид:
и осью симметрии, параллельной оси OY, имеет вид:
а) 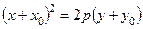 ; б)
; б) 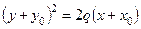 ;
;
в) 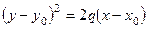 ; г)
; г) 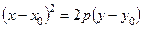 .
.
5. Уравнение гиперболы, не пересекающей ось OY, имеет вид:
а) 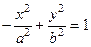 ; б)
; б) 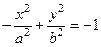 ; в)
; в) 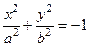 ;
;
г) 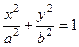 .
.
6. Уравнение 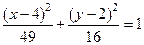 определяет:
определяет:
а) эллипс с полуосями 49 и 16; б) параболу с центром (-4; -2);
в) гиперболу с полуосями 7 и 4; г) эллипс с центром (4; 2).
7. Для любой точки гиперболы постоянной величиной является:
а) модуль разности расстояний до фокусов;
б) сумма расстояний до фокусов;
в) частное расстояний до фокусов; г) расстояние до её центра.
8. Уравнение параболы, ветви которой направлены вниз, имеет вид:
а) 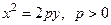 ; б)
; б) 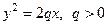 ;
;
в) 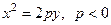 ; г)
; г) 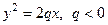 .
.
9. Радиус окружности, заданной уравнением 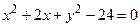 , равен:
, равен:
а) 5; б) 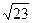 ; в) 2; г) 25.
; в) 2; г) 25.
10. Уравнением 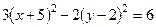 задается:
задается:
а) гипербола с полуосями 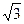 ;
; 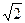 и центром (5; -2);
и центром (5; -2);
б) парабола с вершиной (-5; 2);
в) гипербола с полуосями 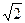 ;
; 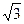 и центром (-5; 2);
и центром (-5; 2);
г) эллипс с центром (5; -2).
11. Выберите линию, которая задается уравнением
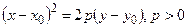
а) 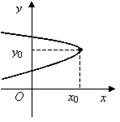 ; б)
; б) 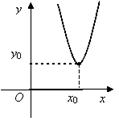 ;
;
в) 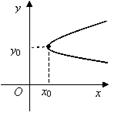 ; г)
; г) 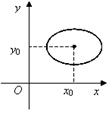 .
.
 МОДУЛЬ 6.
МОДУЛЬ 6.
 2015-01-21
2015-01-21 902
902








