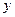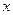|
Параболой называется множество всех точек плоскости, каждая из которых равноудалена от заданной точки этой же плоскости, называемой фокусом, и заданной прямой, называемой директрисой.
 Каноническое уравнение параболы:
Каноническое уравнение параболы:
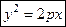 , (12)
, (12)
 где число
где число 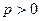 , равное расстоянию от фокуса
, равное расстоянию от фокуса 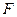 до директрисы
до директрисы 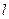 , называется параметром параболы, точка
, называется параметром параболы, точка 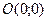 называется вершиной параболы, ось
называется вершиной параболы, ось 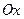 — ось симметрии параболы, координаты фокуса
— ось симметрии параболы, координаты фокуса 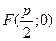 .
.
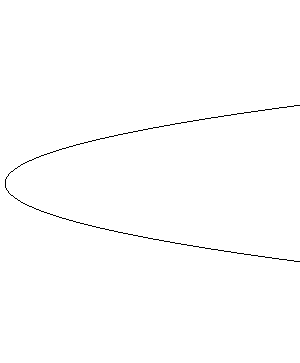 Уравнение директрисы
Уравнение директрисы 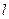 параболы имеет вид
параболы имеет вид 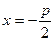 .
.
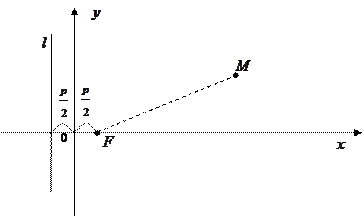

Уравнение 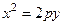 является уравнением параболы, симметричной относительно оси ординат.
является уравнением параболы, симметричной относительно оси ординат.
Уравнения
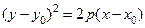 ,
, 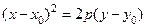 (13)
(13)
также задают параболу, вершина которой задаются точкой 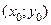 .
.
 Пример 5.4. Уравнение линии приведите к каноническому виду и постройте её:
Пример 5.4. Уравнение линии приведите к каноническому виду и постройте её: 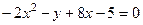 .
.
Преобразуем уравнение: 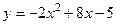 . Выделим в правой части полный квадрат (выделение полного квадрата подробно рассматривалось в примере 5.1):
. Выделим в правой части полный квадрат (выделение полного квадрата подробно рассматривалось в примере 5.1):
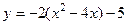 ;
;
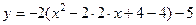 ;
;
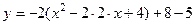 ;
;
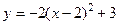 ;
;
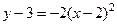 ;
;
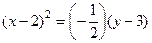 .
.
Получили уравнение параболы (см. (13)) с вершиной в точке (2;3); 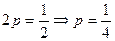 . Прямая
. Прямая 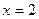 является осью симметрии параболы. Координаты фокуса
является осью симметрии параболы. Координаты фокуса 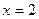 ,
, 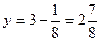 , т.е.
, т.е. 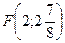 .
.


|
|
|


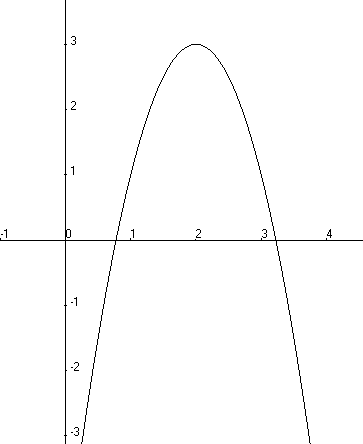
 2015-01-21
2015-01-21 1981
1981