 Первый достаточный признак. Пусть функция
Первый достаточный признак. Пусть функция 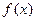 непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 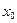 и дифференцируема во всех точках этого интервала (кроме, быть может самой точки
и дифференцируема во всех точках этого интервала (кроме, быть может самой точки 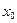 ). Тогда, если:
). Тогда, если:
а) 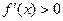 при
при 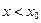 ,
, 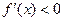 при
при 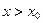 , то в точке
, то в точке 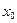 функция
функция 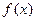 достигает максимума;
достигает максимума;
б) 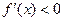 при
при 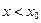 ,
, 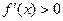 при
при 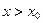 , то в точке
, то в точке 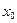 функция
функция 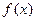 достигает минимума.
достигает минимума.
 Второй достаточный признак экстремума. Пусть функция
Второй достаточный признак экстремума. Пусть функция 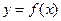 имеет в точке
имеет в точке 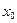 производную
производную 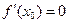 и непрерывную вторую производную
и непрерывную вторую производную 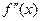 . Тогда, если
. Тогда, если 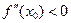 в точке
в точке 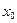 будет максимум, а если
будет максимум, а если 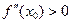 в точке
в точке 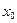 будет минимум.
будет минимум.
Пример 7.14. В примере 7.13 точки 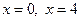 являются точками экстремума. В точке
являются точками экстремума. В точке 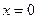 функция достигает максимума, в точке
функция достигает максимума, в точке 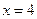 функция достигает минимума.
функция достигает минимума.
Пример 7.15. Издержки предприятия выражаются формулой 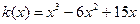 , где
, где 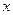 — объём производства. При каком объёме производства средние издержки будут минимальными?
— объём производства. При каком объёме производства средние издержки будут минимальными?
 Средние издержки выражаются формулой
Средние издержки выражаются формулой 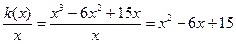 . Найдем минимум этой функции.
. Найдем минимум этой функции.
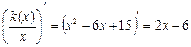 .
.
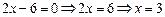 .
.
Найдем вторую производную функции.
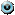
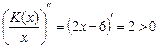 , значит, по второму достаточному признаку экстремума при
, значит, по второму достаточному признаку экстремума при 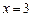 средние издержки достигают минимума.
средние издержки достигают минимума.

 2015-01-21
2015-01-21 5063
5063
