Экстремум функции. Необходимый признак

Точка 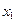называется точкой максимума (maximum) функции 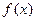, если значение функции в этой точке больше её значений во всех точках некоторого интервала, содержащего точку 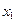, т.е. 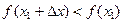для любого 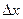( 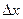— мало по величине).

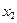Точка называется точкой минимума (minimum) функции 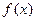, если значение функции в этой точке меньше её значений во всех точках некоторого интервала, содержащего точку 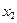, т.е. .

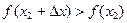Точки, в которых функция достигает максимума или минимума, называются точками экстремума функции, а значения функции в этих точках называют экстремальными.

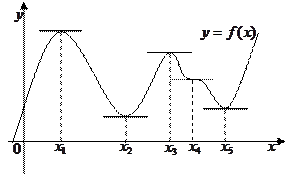
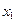Функция, заданная кривой на рисунке выше, в точках и 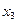достигает максимума, в точках 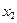и 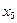— минимума, в точке 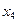— экстремума нет. Очевидно, что функция имеет производную, равную нулю в критических точках. Касательная к кривой в этих точках параллельна оси .

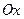Необходимый признак экстремума. Если дифференцируемая функция достигает в некоторой точке экстремума, то её производная в этой точке равна нулю или не существует.