 Если для всех точек отрезка
Если для всех точек отрезка 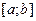 при
при 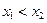 выполняется равенство
выполняется равенство 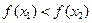 , то функция
, то функция 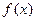 называется возрастающей на
называется возрастающей на 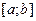 .
.

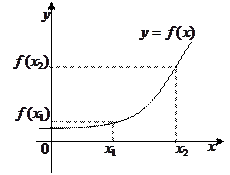
При выполнении условий 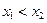 ,
, 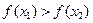 функция
функция 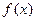 называется убывающей на
называется убывающей на 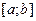 .
.

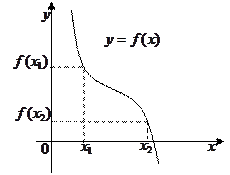
Интервалы, в которых функция 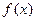 только возрастает или только убывает, называются интервалами монотонности функции.
только возрастает или только убывает, называются интервалами монотонности функции.
 Признак возрастания. Дифференцируемая функция
Признак возрастания. Дифференцируемая функция 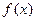 возрастает на отрезке
возрастает на отрезке 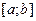 тогда и только тогда, когда её производная
тогда и только тогда, когда её производная 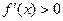 .
.
 |
 Признак убывания. Дифференцируемая функция
Признак убывания. Дифференцируемая функция 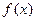 убывает на отрезке
убывает на отрезке 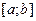 тогда и только тогда, когда её производная
тогда и только тогда, когда её производная 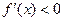 .
.
В точках, отделяющих интервалы монотонности функции, производная функции обращается в нуль или не существует. Эти точки называются критическими.
Для нахождения интервалов монотонности функции 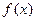 необходимо найти все её критические точки и установить знак производной в каждом из интервалов, на которые критические точки разбивают область существования функции.
необходимо найти все её критические точки и установить знак производной в каждом из интервалов, на которые критические точки разбивают область существования функции.
Пример 7.13. Найдите интервалы монотонности функции 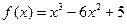 .
.
 Функция определена на всей числовой оси. Найдём её производную.
Функция определена на всей числовой оси. Найдём её производную. 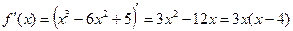 .
.
Найдём критические точки, приравняв производную к нулю.
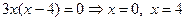 — критические. Результаты исследования занесём в таблицу:
— критические. Результаты исследования занесём в таблицу:
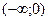 | 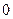 | 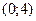 | 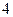 | 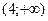 | |
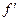 | + | 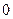 | 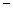 | 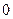 | + |
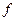 |  | 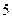 |  | 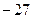 |  |
 Таким образом, функция
Таким образом, функция 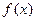 возрастает а интервалах
возрастает а интервалах 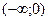 и
и 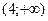 , а убывает на интервале
, а убывает на интервале 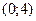 .
.

 2015-01-21
2015-01-21 1374
1374
