2014-10-30
731
Неразрывным сплошным движением жидкости называется такое движение, когда внутри потока отсутствуют пустоты, нет разрыва струи.
Рассмотрим русло. В русле поток жидкости.
Выделим в русле элементарный прямоугольный параллелепипед с ребрами dx, dy и dz (параллелепипед неподвижен относительно стенок русла). Через стенки параллелепипеда течет сжимаемая жидкость (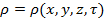
.
 |
 |
 |
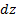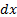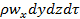| X |
| Y |
| Z |
 |
 |
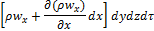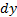Для составления ОБС определяем прежде всего субстанцию, для которой составляется ОБС; в качестве таковой служит масса жидкости.
Пространственным контуром является прямоугольный параллелепипед неподвижный относительно стенок русла.
Временной интервал – элементарный промежуток времени -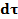 
.
В условиях неразрывности потока жидкости действует закон сохранения массы, поэтому из ОБС выпадают Источники и Стоки: +Пр – Ух = Нак
Составляем ОБС для параллелепипеда за время dt в направлении оси Х (потом Y и Z – по аналогии).
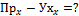
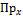– приход жидкости, показывает массу жидкости которая вошла через левую грань параллелепипеда за время dt:
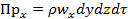, где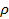 
- плотность жидкости, которая может изменяться во времени и по координатам; 
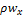– удельная массовая скорость жидкости.
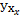– уход жидкости, показывает сколько жидкости вышло через правую грань за время dt:
.
.
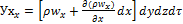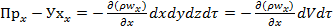По аналогии записываем разности приходов и уходов для двух других направлений:
; 
;
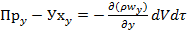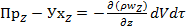Таким образом левая часть ОБС представляет собой выражение:
.
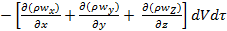Остается выразить правую часть ОБС, а именно: Накопление массы жидкости в контуре за время dt. Количество массы в объеме параллелепипеда в момент времени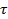 
равно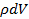 
. Полагая, что плотность жидкости является функцией только времени (в пределах выделенного объема), то Накопление массы жидкости в объеме параллелепипеда к моменту времени 
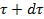записывается в частных производных:
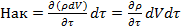(т.к. выделенный объем неизменен).
Собирая теперь найденные выше элементы ОБС, получаем после упрощения уравнение неразрывности в виде
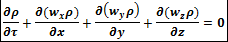
Решение системы уравнений Навье-Стокса для частного случая: жидкость идеальна (m=0); несжимаемая (капельная ρ=const); среди внешних массовых сил действует только сила тяжести; движение жидкости стационарное и безвихревое. Диаграмма Бернулли для идеальной жидкости.
(безвихревое,– отсутствует вращательная составляющая жидкой частицы 
)
Для указанных условий решение уравнений Навье – Стокса получают в виде интеграла Бернулли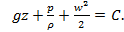 
Каждый член уравнения имеет определенный физический смысл. (Размерность каждого члена этого уравнения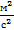 
. Умножим числитель и знаменатель на кг. Тогда получим размерность удельной энергии 
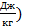В этом случае первый член – удельная потенциальная энергия положения жидкости; второй – удельная потенциальная энергия давления жидкости; третий – удельная кинетическая энергия жидкости. Сумма этих удельных энергий представляет собой полную удельную энергию жидкости, которая одинакова в любом сечении потока.
Поделив обе части уравнения Бернулли на g, получим
.
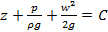В практическом смысле уравнение Бернулли принято записывать для двух сечений потока
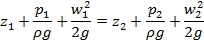
Размерность каждого члена уравнения – метр. Следовательно, существует и геометрический смысл каждого члена уравнения Бернулли: первый – нивелирная высота, второй – пьезометрическая высота, третий – скоростная высота. Сумма указанных высот потока идеальной жидкости при плоскости отсчета взятой произвольно, не зависит от выбранного сечения, т.е. остается величиной постоянной. Наряду с термином «высота» в гидравлике для этих слагаемых используют термин «напор». Сумму трех слагаемых называют полным напором.
На рисунке представлена графическая интерпретация уравнения Бернулли для безвихревого потока идеальной жидкости в форме так называемой диаграммы Бернулли.
 |
 |
 |
 |
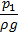| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| С |
| С |
| В |
| В |
| А |
| А |
| Z1 |
| Z2 |
| Z3 |
| 0 |
| 0 |
 |
 |
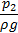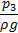| Диаграмма Бернулли для безвихревого потока идеальной жидкости в прямом трубопроводе постоянного поперечного сечения: О – О линия плоскости отсчета; А – А линия нивелирных высот; В – В линия пьезометрических высот; С – С линия полного напора. |
При решении задач это уравнение должно быть дополнено уравнением неразрывности в интегральной форме.
