Сетевые модели

Сетевая модель отображает взаимосвязи операций и порядок их выполнения. Операции логически упорядочены во времени в том смысле, что одни операции нельзя начать, прежде чем не будут завершены другие. Операция – это работа, для выполнения которой требуются затраты времени и ресурсов.

С применением сетевых моделей решается широкий круг задач оптимизации планирования и претворения в жизнь взаимосвязанных процессов. Такие задачи возникают при осуществлении проектов любой сложности, включающих проведение некоторого комплекса мероприятий. Освоение инструмента «оптимизации на сетях» особенно актуально в связи с развитием процессного подхода к совершенствованию управленческой деятельности.

Цели решения задач заключаются:

• в определении критического пути (метод критического пути — МКП), т.е. маршрута или набора взаимосвязанных, «критических» операций, которые особым образом влияют на общую продолжительность выполнения проекта и которым необходимо уделять особое внимание для выполнения проекта в срок;

• определении и расчете резерва времени, под которым понимается количественный показатель подвижности, или запасного времени по каждому действию в сетевой модели при условии обязательного завершения проекта в минимально возможные сроки;

• планировании человеческих и материальных ресурсов с позиции их равномеризации во времени;

• сокращении времени выполнения проекта с учетом экономических факторов использования имеющихся ресурсов;

• оценке и пересмотре планов (программ) при условии случайной продолжительности выполнения операций (ПЕРТ).

В методах ПЕРТ и МКП основное внимание уделяется временному аспекту планов. Оба метода определяют календарный план проекта. Различие состоит в том, что в методе МКП продолжительность операций определяется детерминированными величинами, а в методе ПЕРТ – случайными. Оба метода составляют единый метод сетевого планирования и управления (СПУ).

Сетевые модели имеют множество модификаций. В качестве классификационных признаков используют структуру, характер информации, количество учитываемых параметров, количество выделяемых работ. По структуре сетевые модели делятся на канонические и альтернативные. Канонические модели отличаются фиксированной структурой. Это означает, что во всех вершинах над работами осуществляется единственная логическая операция «И» (V), согласно которой любую выходящую из события работу можно начать лишь после завершения всех без исключения входящих в нее работ.

В альтернативных моделях структура сети переменная. В любой вершине допускаются операции логики «И» (V), либо «ИЛИ» ^). В последнем случае для начала выходящей из события работы достаточно окончания любой из входящих в него работ. В зависимости от того, какие ограничения наложены на описание событий (вершин) и операций (дуг), выделяют: сети простого типа, вершины которых не имеют внутренней структуры; иерархические сети, вершины которых рекурсивно сами обладают сетевой структурой.

Сетевые модели могут быть вероятностными и детерминистическими. Вероятностными считаются сетевые модели, в которых параметры работ заданы случайными величинами, детерминистическими – те, в которых эти параметры заданы однозначно обусловленными величинами. По составу учитываемых в сетевых моделях параметров выделяют модели с учетом времени, стоимости и ресурсов, а именно одно- и многопараметрические. В зависимости от количества технологически независимых комплексов работ сетевые модели подразделяют на одно- и многосетевые. Односетевые модели могут быть одно- и многоцелевыми, многосетевые модели – всегда многоцелевые.

Не исключаются и другие классификации, что зависит от назначения сетевых моделей. В настоящее время они широко применяются при проектировании и оптимизации коммуникационных систем, экономико-информационных и информационно-управляющих систем, сетевого управления и в других приложениях.

Техника построения сетевой модели заключается в следующем. Сеть или ориентированный конечный граф без контуров состоят из множества узлов (вершин, точек) и дуг (ребер, звеньев), соединяющих различные пары узлов. На каждой дуге задана ее ориентация (определено направление), поэтому говорят, что сеть является ориентированной. В описании ориентированной сети используют числа натурального ряда для обозначения узла (Е_i) и пару чисел, определяющих исходящий (i) и входящий (j) узлы для ориентирования дуги (i, j). Последовательность дуг, соединяющих узлы, называется путем между этими узлами. Сеть называют связной при условии, что существует, по крайней мере, один путь между любой парой узлов.

Построение сетевой модели должно следовать определенным правилам:

• каждая операция в сети представляется только одной дугой (i, j);

• ни одна пара операций не должна определяться одинаковыми начальными и конечными событиями;

• при включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы: какие операции необходимо завершить непосредственно перед началом рассматриваемой операции; какие операции должны следовать после завершения данной операции; какие операции могут выполняться одновременно?

• в сети не должно быть событий (кроме исходного), в которые не входит ни одна дуга, и событий (кроме завершающего), из которых не выходит ни одна дуга.

В построении модели используют три вида операций (рис. 21):

1) действительная операция – работа, требующая затрат времени и ресурсов (сплошная линия);

2) операция-ожидание, т.е. работа, требующая только затраты времени (штрих-пунктирная линия);

3) фиктивная операция – логическая связь, которая отражает технологическую или ресурсную зависимость с отсутствием связывающих их операций (пунктирная линия).

Построение сетевой модели начинается с составления списка операций (работ), подлежащих выполнению. Последовательность операций в списке может быть произвольной, так как построение сетевой модели проходит несколько итераций. Перечень операций тщательно продумывается и детализируется. Операции, включенные в список, характеризуются определенной продолжительностью, которая устанавливается на основе действующих нормативов или по аналогии. Такие временные оценки называются детерминированными.

Список операций представляется в виде таблицы, в которой указываются индекс мероприятия, его содержание, очередность и продолжительность. После составления списка операций приступают к процедуре построения сети, фрагмент которой приведен на рис. 21.

Дополнением к планированию работ по проекту служит построение графика Ганта и диаграммы распределения потребностей в человеческих и материальных ресурсах. График Ганта дает возможность пользователю определить, какие действия имеют место в любой отрезок времени. Диаграмма потребностей позволяет проанализировать варианты распределения ресурсов, особенно при возникновении проблем с выполнением запланированных мероприятий. Если существуют ограничения на расход ресурсов и по диаграмме выяснено их превышение, то необходимо изыскать возможности «выровнять» (равномеризировать) потребности на протяжении проекта, особенно когда речь идет о рабочей силе. Такие действия потребуют корректирования первоначального варианта диаграммы Ганта.

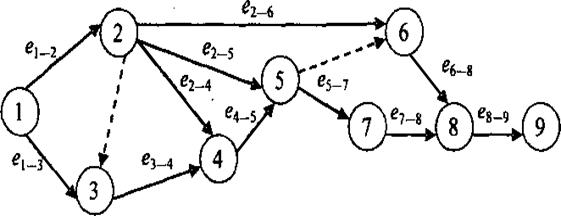
Рис. 21. Фрагмент сетевой модели