 Постановка задачи. Рассмотрим изотропное неравномерно нагретое тело, объем которого
Постановка задачи. Рассмотрим изотропное неравномерно нагретое тело, объем которого 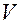 , а поверхность
, а поверхность 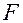 Выделим в этом теле элементарный объем d
Выделим в этом теле элементарный объем d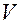 , ограниченный поверхностью d
, ограниченный поверхностью d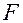 . Выделенный элементарный объем d
. Выделенный элементарный объем d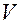 настолько мал, что изменением температуры внутри его по координатам можно пренебречь, учитывая лишь изменение температуры во времени. Требуется найти закономерность измерения температуры в твердом теле t = f (x, y, z, t).
настолько мал, что изменением температуры внутри его по координатам можно пренебречь, учитывая лишь изменение температуры во времени. Требуется найти закономерность измерения температуры в твердом теле t = f (x, y, z, t).
Выделенный объем d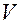 будем рассматривать в качестве термодинамической системы. Запишем для нее первый закон термодинамики. d
будем рассматривать в качестве термодинамической системы. Запишем для нее первый закон термодинамики. d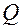 = d
= d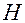 + d
+ d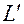 , где d
, где d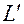 = -
= - 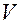 d
d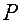 – работа сил упругих деформаций в твердом теле при постоянном давлении равна нулю. Теплота d
– работа сил упругих деформаций в твердом теле при постоянном давлении равна нулю. Теплота d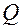 представляет собой сумму теплоты, выделяемой внутри объема тела (
представляет собой сумму теплоты, выделяемой внутри объема тела (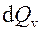 ), и теплоты, поступающей через поверхность извне (
), и теплоты, поступающей через поверхность извне ( ), т.е.
), т.е. 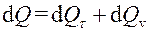 . Тогда
. Тогда
 .
.
Количество теплоты, проходящей через поверхность тела за время dt:
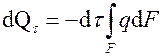 .
.
Знак минус появился потому, что теплота теряется объемом, т.е. с точки зрения термодинамики теплота отрицательная. Теплота, выделяемая внутри объема тела за время dt, определяется по формуле
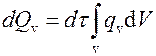 .
.
Изменение энтальпии за время dt:

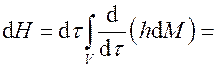
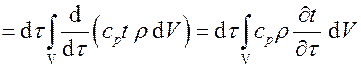 .
.
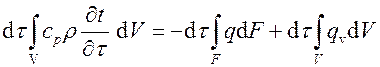
сокращая на dt, имеем
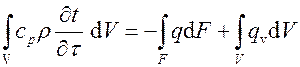 .
.
Воспользуемся теоремой Остроградского-Гаусса, согласно которой интеграл потока вектора поля через замкнутую поверхность F равен
интегралу от дивиргенции этого потока вектора поля по объему V, ограниченному поверхностью F, т.е.
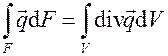 .
.
Тогда уравнение запишется в виде
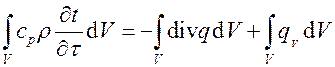
или 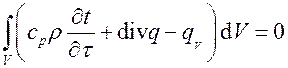 .
.
Учитывая, что интеграл равен нулю, когда его подынтегральное выражение равно нулю, имеем
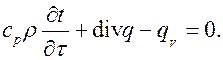
Подставляя значения q, получим
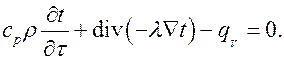
Учитывая, что  , запишем
, запишем
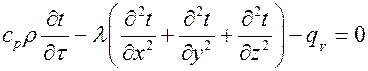 ,
,
откуда
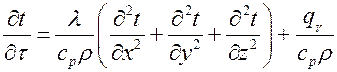 .
.
Величина 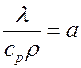 , м2/с, называется коэффициентом температуропроводности, является физическим параметром и характеризует теплоинерционные свойства тела. Уравнение
, м2/с, называется коэффициентом температуропроводности, является физическим параметром и характеризует теплоинерционные свойства тела. Уравнение
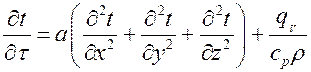
является дифференциальным уравнением теплопроводности для твердого тела.
 2014-04-09
2014-04-09 1607
1607







