2014-04-09
1289
Постановка задачи. Имеется вертикальная стенка, ее температура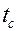 
= const. Стенка омывается жидкостью, температура которой вдали от стенки 
= const (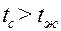
). Процесс стационарный. 
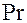= 1, т.е. 
.
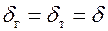Требуется получить формулы для расчета локального и среднего коэффициентов теплоотдачи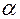 
(безразмерного числа Nu).
При решении задачи сделаем следующие допущения: стенка вдоль осей x и z бесконечная; силы инерции малы по сравнению с силами тяжести и вязкости; перенос теплоты конвекцией и теплопроводностью вдоль движущегося слоя жидкости (оси x) мал, и им пренебрегаем; градиент давления в пограничном слое равен нулю; физические параметры жидкости (исключая плотность) не зависят от температуры, а плотность является линейной функцией температуры.
Для нахождения коэффициента теплоотдачи от стенки к жидкости воспользуемся дифференциальным уравнением теплоотдачи
,
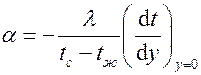в котором неизвестен градиент температуры жидкости вблизи стенки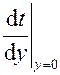 
.Опытным путем было установлено, что температура в пристенном слое изменяется по параболическому закону
|
|
|
,
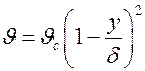где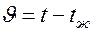 
, 
.
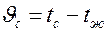Тогда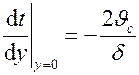 
.Подставляем это значение в дифференциальное уравнение теплоотдачи, получаем
.
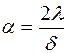Таким образом, чтобы найти 
, нужно знать закономерность изменения толщины пограничного слоя по высоте стенки 
. Для этого выделим участок поверхности стенки высотой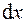 
, а по оси z размер стенки возьмем равным единице.
Тепловой поток, который отдается от этого участка стенки в процессе теплоотдачи, определится по формуле 
, этот же тепловой поток можно рассчитать по формуле 
:
,
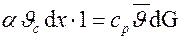где 
– средняя интегральная температура жидкости в пограничном слое; d
– элементарный расход массы жидкости через сечение площадью (
∙1). Подставим в формулу значение 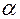и выразим dв виде
.
Из уравнения неразрывности потока элементарный расход жидкости
.
Приравняем формулы, получим
.
В этой формуле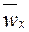 
– средняя интегральная скорость и 
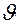– средняя интегральная температура жидкости по сечению пограничного слоя не известны. Найдем:
.
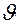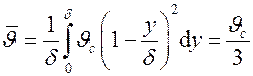Для определения 
определим закономерность изменения скорости в пограничном слое. Для этого воспользуемся дифференциальным уравнением движения в проекции на ось x, которое в силу принятых нами упрощений будет иметь вид
.
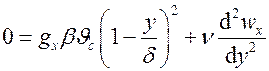Решая это уравнение совместно с граничными условиями: при
y = 0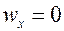 
; при y = δ 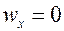, получаем закономерность изменения скорости в пограничном слое
.
Находим среднюю интегральную скорость потока в сечении пограничного слоя:
.
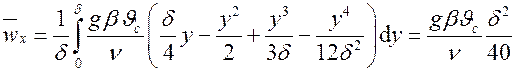Подставим в формулу элементарного расхода жидкости получим
.
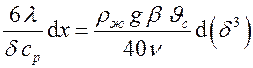Перенесем d из левой части уравнения в правую и продифференцируем, а затем проинтегрируем обе его части. Получим
,
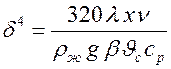откуда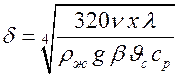 
.
|
|
|
Подставим значение 
в формулу коэффициента теплоотдачи
.
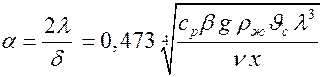Приведем это уравнение к безразмерному виду. Для этого умножим левую и правую части на 
, тогда
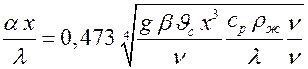, или
.
Локальный коэффициент теплоотдачи 
. Определим средний коэффициент теплоотдачи:
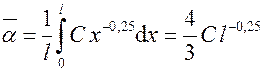, т.е. 
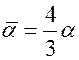. Тогда
.
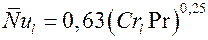Формула получена при ряде упрощений, поэтому ее необходимо скорректировать с учетом опытных данных.
Расчетные формулы. Для расчета местных коэффициентов теплоотдачи при свободном ламинарном течении жидкости вдоль вертикальной стенки необходимо использовать формулу
.
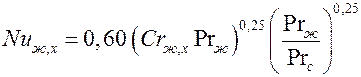Расчет среднего коэффициента теплоотдачи рекомендуется вести по формуле
.
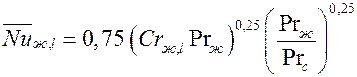За определяющий размер при расчете локального коэффициента теплоотдачи принята координата x, отсчитываемая от места начала теплообмена, а при расчете среднего коэффициента теплоотдачи – высота стенки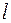 
. Определяющая температура .
