Отыскание вектора конечной продукции

Для решения второй задачи межотраслевого баланса запишем модель Леонтьева в матричном виде

АХ + Y = Х,

откуда получим выражение (3.9)

Y = (Е – А) × Х.

Пример. Три отрасли выпускают продукцию, причем нормы затрат ресурсов заданы матрицей А, вектор валовой продукции – Х:

А = 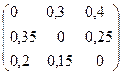, Х =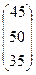

Определить вектор конечной продукции Y (рис. 67).

При определении венктора Y используется функция Excel =МУМНОЖ из категории Математические, позволяющая получить результат перемножения матрицы Е-А и вектора Х.

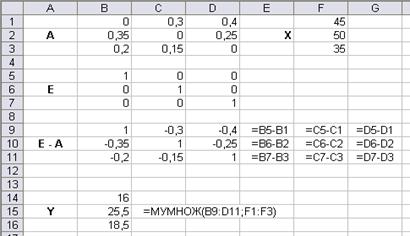
Рис. 67. Расчёт вектора конечной продукции

Пример оптимизационной модели отыскания вектора конечной продукции (рис. 68 – 70).

Систему уравнений межотраслевого баланса можно представить в виде Х = В ×Y или

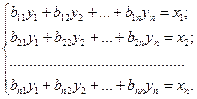
тогда, в качестве целевой функции задачи оптимизации можно выбрать максимизацию объёма конечной продукции

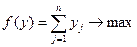
при ограничениях

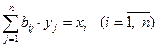
и условии неотрицательности получаемого решения

y_j ³ 0 .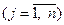

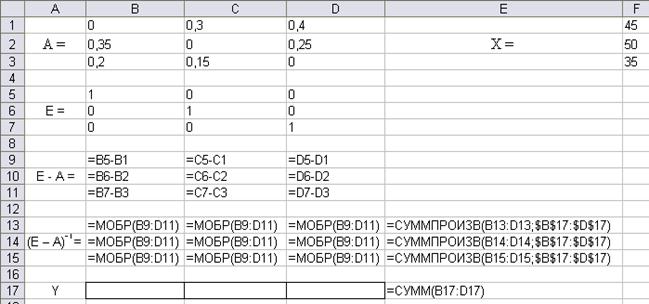
Рис. 68. Ввод исходных данных в модель оптимизации

Выделим ячейки B17:D17 для размещения искомых переменных y₁, y₂ и y₃. Математические выражения левых частей ограничений введём в ячейки Е13:Е15 с помощью функции =СУММПРОИЗВ из категории Математические. Целевую функцию, как сумму искомых переменных введём в ячейку Е17. Заполним диалоговое окно программы Поиск решения из меню Сервис (рис. 69).

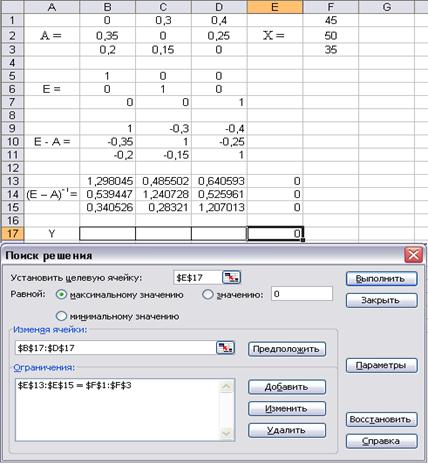
Рис. 69. Заполнение диалогового окна Поиска решения

Нажав на кнопку Параметры в диалоговом окне надстройки Поиск решения, укажем с помощью “галочек”: Линейная модель и Неотрицательные значения. Результаты отыскания вектора конечной продукции Y представлены на рис. 70.

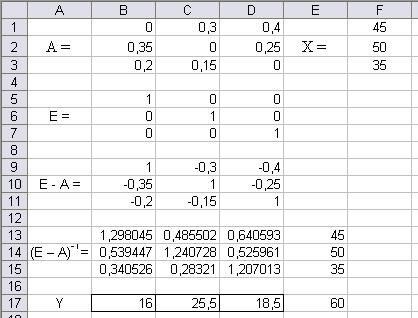
Рис. 70. Результата решения задачи межотраслевого баланса