Для решения третьей задачи баланса все отрасли разделим на две группы. К первой группе отнесем отрасли, для которых задан конечный продукт. Множество номеров этих отраслей обозначим индексами i, j = 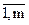 . Ко второй группе отнесем отрасли, для которых задан валовой выпуск. Множество номеров этих отраслей обозначим индексами i, j =
. Ко второй группе отнесем отрасли, для которых задан валовой выпуск. Множество номеров этих отраслей обозначим индексами i, j = 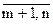 . Тогда вектор валовых выпусков можно разделить на два подвектора
. Тогда вектор валовых выпусков можно разделить на два подвектора
Х = 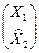 , (5.11)
, (5.11)
где Х1 – искомый подвектор с элементами Хi(i = 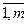 );
);

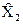 - заданный подвектор с элементами Хi(i =
- заданный подвектор с элементами Хi(i = 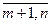 ).
).
Аналогично вектор конечного продукта можно разделить на два подвектора
Y = 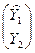 , (5.12)
, (5.12)
где 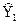 – подвектор с известными значениями Yi(i =
– подвектор с известными значениями Yi(i = 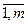 );
);
Y2 - подвектор с неизвестными значениями
Yi(i = 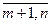 ).
).
Матрица А разбивается на четыре подматрицы
А = 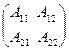 , (5.13)
, (5.13)
где А11 – подматрица с элементами аij (i, j = 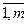 );
);
А12 – подматрица с элементами аij (i = 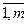 ; j =
; j = 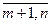 );
);
А21 – подматрица с элементами аij (i = 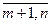 ; j =
; j = 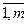 );
);
А22 – подматрица с элементами аij (i, j = 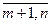 ).
).
Для нахождения неизвестных подвекторов Х1 и Y2, зная А, 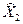 ,
, 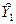 , представим модель Леонтьева в следующем виде:
, представим модель Леонтьева в следующем виде:
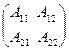 ×
× 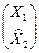 +
+ 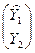 =
= 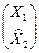 . (5.14)
. (5.14)
Раскроем это выражение
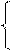 А11Х1+А12
А11Х1+А12 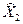 +
+ 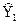 = Х1 (5.15)
= Х1 (5.15)
А21Х1+А22 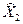 +Y2=
+Y2= 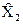 .
.
Из первого уравнения этой системы найдем
Х1 = (Е – А11)-1 × (А12 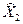 +
+ 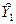 ). (5.16)
). (5.16)
Из второго уравнения найдем
Y2 = (Е – А22) × 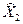 - А21 Х1 . (5.17)
- А21 Х1 . (5.17)
Найдя из выражения (3.16) Х1 и подставив в выражение (3.17), получим Y2.
Пример. Три отрасли выпускают продукцию, причем нормы затрат ресурсов заданы матрицей А:
А = 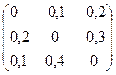 .
.
Конечный продукт первой отрасли равен 8 ед., объем производства второй отрасли равен 10 ед., а третьей – 15 ед. Определить объем производства первой отрасли и конечный продукт второй и третьей.
Решение. Согласно изложенному ранее первая отрасль входит в первую группу, а вторая и третья – во вторую группу, тогда
Х = 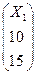 ,
, 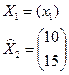 , Y =
, Y = 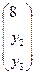 ,
, 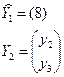
А11 = (0) А12 = (0,1 0,2)
А21 = 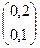 А22 =
А22 = 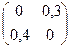 .
.
Из формулы (16) найдем
Х1 = (1 - 0)-1 × [(0,1 0,2) × 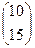 + 8] = 12
+ 8] = 12
Из формулы (3.17) найдем
Y2 = 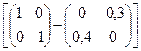 ×
× 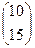 -
- 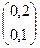 × 12 =
× 12 = 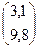 .
.
Таким образом, валовой выпуск первой отрасли равен 12 ед., конечный продукт второй и третьей равен 3,1 ед. и 9,8 ед. соответственно.
 2015-01-30
2015-01-30 471
471








