По десяти шахтам известны следующие данные, характеризующие процесс добычи угля.
Таблица 1
| Номер шахты, i | ||||||||||
Мощность пласта, 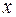 (м) (м) | ||||||||||
Сменная добыча угля на одного рабочего, 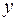 (т) (т) |
1. Постройте поле корреляции и по виду облака рассеяния сделайте предположение о форме связи между переменными 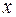 и
и 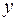 .
.
Рассчитайте характеристики случайных величин:
2. средние значения 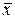 ,
, 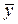 ;
;
3. выборочные дисперсии (вариации) var (x), var (y);
4. стандартные (среднеквадратические) отклонения S (x), S (y);
5. выборочную ковариацию (выборочный корреляционный момент) cov (x, y);
6. выборочный коэффициент корреляции rxy.
7. С помощью этих характеристик оцените степень рассеяния случайных величин вокруг средних значений и тесноту связи переменных.
Решение.
Для удобства вычислений составим таблицу
Таблица 2
| i | xi | уi | 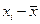 | 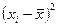 | 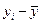 | 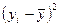 | хi· уi |
| -1,4 | 1,96 | -1,8 | 3,24 | ||||
| 1,6 | 2,56 | 3,2 | 10,24 | ||||
| 2,6 | 6,76 | 3,2 | 10,24 | ||||
| -0,4 | 0,16 | 0,2 | 0,04 | ||||
| -1,4 | 1,96 | -1,8 | 3,24 | ||||
| -1,4 | 1,96 | -0,8 | 0,64 | ||||
| -0,4 | 0,16 | -0,8 | 0,64 | ||||
| -0,4 | 0,16 | -1,8 | 3,24 | ||||
| -1,4 | 1,96 | -0,8 | 0,64 | ||||
| 2,6 | 6,76 | 1,2 | 1,44 | ||||
| Итого | 24,4 | 33,6 | |||||
| Среднее значение | 9,4 | 6,8 | 2,44 | 3,36 | 66,4 |
1. Построим поле корреляции (диаграмму рассеяния) по данным 2 и 3 столбцов таблицы
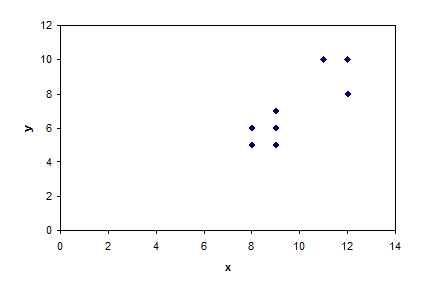
Рисунок 1. Поле корреляции
По виду облака рассеяния предположим линейную форму связи между переменными 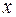 и
и 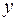 .
.
2. По формулам (1.3) рассчитаем средние значения 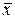 ,
, 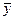 .
.
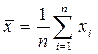 ,
, 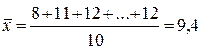 (см. столбец 2 таблицы);
(см. столбец 2 таблицы);
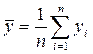 ,
, 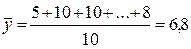 (см. столбец 3 таблицы).
(см. столбец 3 таблицы).
3. Для вычисления выборочных дисперсий (вариаций) var (x), var (y) используем формулы (1.5).
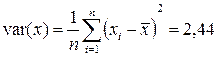 (см. столбцы 4 и 5 таблицы);
(см. столбцы 4 и 5 таблицы);
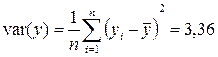 (см. столбцы 6 и 7 таблицы).
(см. столбцы 6 и 7 таблицы).
4. Стандартные (среднеквадратические) отклонения S (x), S (y) найдем по формулам (1.6)
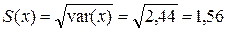 ,
,
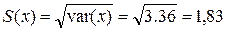 .
.
5. Выборочная ковариация (выборочный корреляционный момент) cov (x, y) находится по формуле (1.8). Среднее произведений вычисляется в 8 столбце таблицы, из него вычитается произведение средних.
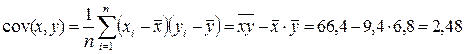 .
.
6. Вычислим выборочный коэффициент корреляции rxy по формуле (1.7):
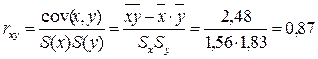 .
.
7. Степень рассеяния величин 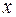 и
и 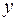 вокруг средних значений
вокруг средних значений 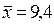 (м),
(м), 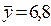 (т) хорошо характеризуют стандартные отклонения
(т) хорошо характеризуют стандартные отклонения 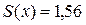 (м) и
(м) и 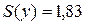 (т). Рассеяние
(т). Рассеяние 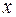 находится в пределах 17%, а рассеяние
находится в пределах 17%, а рассеяние 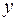 – 27%. По выборочной ковариации можно судить о зависимости двух случайных величин, их небольшом рассеянии относительно среднего значения. Коэффициент корреляции
– 27%. По выборочной ковариации можно судить о зависимости двух случайных величин, их небольшом рассеянии относительно среднего значения. Коэффициент корреляции 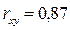 , величина которого близка к единице, говорит о наличии сильной линейной зависимости между переменными
, величина которого близка к единице, говорит о наличии сильной линейной зависимости между переменными 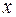 и
и 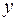 .
.
 2015-01-30
2015-01-30 1499
1499








