2015-01-30
998
Имеются статистические данные за ряд лет о доходах домашних хозяйств и их расходах на местный автотранспорт.
Таблица 7
| Номер наблюдения, i | Доход домашнего хозяйства, 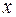 ($) | Расходы домашнего хозяйства на местный автотранспорт,  ($) |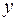
| 695,2 | 3,1 | |
| 751,9 | 3,3 | |
| 810,3 | 3,4 | |
| 3,6 | ||
| 998,1 | ||
| 1096,2 | 4,4 | |
| 1194,3 | 4,7 | |
| 1313,5 | ||
| 1474,3 | 5,5 | |
| 1650,5 | 6,2 | |
| 1828,7 | 6,3 | |
| 2040,9 | 6,2 | |
| 2180,1 | 6,6 | |
| 2333,2 | 6,6 |
1. Постройте линейную регрессионную модель связи переменных, где 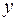интерпретируется как объясняемая переменная, а 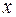– объясняющая, используя оценки наименьших квадратов.
2. Рассчитайте линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
3. Оцените статистическую значимость параметров регрессии и корреляции на уровне значимости α =0,05 с помощью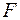 
-критерия Фишера и 
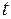-критерия Стьюдента.
4. Выполните прогноз заработной платы 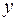при прогнозном значении среднедушевого прожиточного минимума 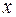, составляющем 110% от среднего уровня.
5. Оцените точность прогноза, рассчитав 95% доверительные интервалы для среднего и индивидуального значения объясняемой переменной при том же значении .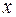
6. Найдите с надежностью 0,95 интервальные оценки параметров уравнения регрессии α и β.
7. На одном графике (графике подбора) постройте исходные данные и теоретическую прямую. Сделайте вывод.
