Решение. При тех же условиях (1) найдем ско­рость и1 плиты в момент времени t1 = 2 с

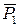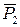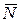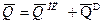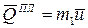При тех же условиях (1) найдем ско­рость и₁ плиты в момент времени t₁ = 2 с. Рассматриваем опять механическую систему, состоящую из плиты и груза, и изображаем действующие на нее внешние силы , и реакцию ; проводим оси ху (рис. 7.8). Восполь­зуемся теоремой об изменении количества движения системы, учитывая, что для рассматриваемой системы , где и 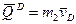– количества движения плиты и груза соответственно. Составляя уравнение в проекции на ось х, 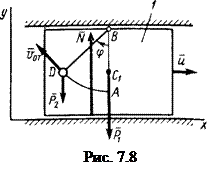получим:

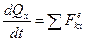, или ,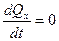

так как

.

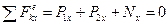Отсюда следует, что

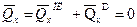или

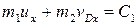(6)

Для определения v_Dx рассмотрим движение груза как сложное, счи­тая его движение по отношению к плите относительным, а движение са­мой плиты – переносным движением. Тогда 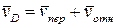, где числен­но 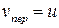и 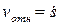. Покажем вектор 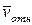(рис. 7.8), направив его перпендикулярно BD в сторону положительного отсчета s или φ, и опреде­лим проекцию вектора 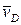на ось х; получим:: v_Dx = u_х -u_отн cos φ, где

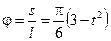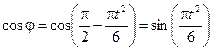и . (7)

В данной задаче v_Dx можно еще найти, определив абсциссу точки D, т.е. 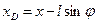(рис. 7.7); тогда 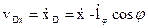, где 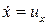, , 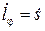а значение cos φ дает равенство (7).

При найденном значении v_Dx равенство (6), если учесть, что и_х = и, а 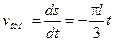, примет вид:

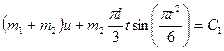. (8)

По начальным условиям при t = 0 и = 0, что дает С₁ = 0, и оконча­тельноиз (8) находим:

.

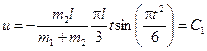Этот результат определяет зависимость и от t. Полагая здесь t = t₁ = 2 с, найдем искомую скорость u₁.

Ответ: и₁ = -0,48 м/с (скорость направлена влево).

3. Определение реакции N₁