Критические параметры. Приведенная скорость

Важной характеристикой потока сжимаемой среды является скорость распространения малых возмущений, или скорость звука, в нем.

В зависимости от того, будет ли скорость движения газа меньше или больше скорости звука, принципиально различными будут и происходящие в среде явления. Продемонстрируем это на простом примере. Предположим, что из баллона большой емкости через сужающийся патрубок происходит истечение газа в камеру. Пусть сначала 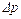между баллоном и камерой невелика и скорость истечения меньше скорости звука.

Будем медленно понижать давление в камере, тогда скорость истечения начнет повышаться. Создаваемые в камере возмущения (уменьшения) давления будут распространяться против течения из камеры через патрубок в баллон до тех пор, пока скорость в выходном сечении патрубка не достигнет скорости звука. После этого возмущения давления не смогут уже проникнуть в баллон, т.к. они будут сноситься потоком, имеющим ту же скорость, что и скорость распространения возмущений в газе. Дальнейшее понижение давления в камере не отразится на истечении, скорость которого будет оставаться постоянной и равной скорости звука в выходном сечении патрубка. Это явление называется "запирание потока".

Если в каком-нибудь сечении потока скорость достигает значениия, равного местной скорости звука, то сечение называют критическим. Скорость потока в критическом сечении называют критической (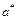). Критическими также называют и соответствующие значения давления, плотности и температуры ().

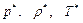В адиабатическом движении газа критические значения параметров состояния одинаковы для всего объема газа, и могут быть определены, например, по "заторможенным" значениям параметров в баллоне. Наличие критических явлений представляет характерную особенность газовых течений.

Для определения критических параметров воспользуемся тем, что при V = а^* число Маха равно единице. Тогда из (2.5)...(2.7) получим

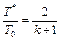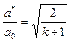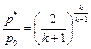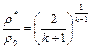; ; ; . (2.8)

Отношение скорости потока в данной точке к одинаковой для всего потока в целом критической скорости 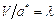называют скоростным коэффициентом (приведенной скоростью).

Параметры потока газа могут быть выражены через скоростной коэффициент (приведенную скорость) .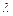

.

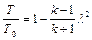Максимальной скорости потока при Т = 0 соответствует

.

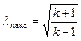Между М и 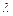имеется связь. Для ее установления уравнение (2.4) запишем через критическую скорость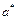

.

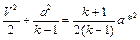Разделив обе части этого равенства на 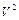, получим

,

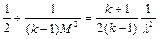
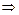
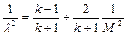или

; .

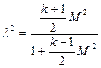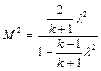Ниже представлены зависимости от приведенной скорости:

× полного давления ;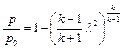

× плотности ;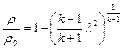

× скорости потока .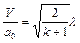

Учитывая, что параметры торможения постоянны для всех точек данного потока газа, из ранее приведенных равенств получим отношение параметров для двух (обозначенных индексами ₁ и ₂) произвольных сечений данного потока, если известны в этих сечениях М или :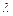

;

;

;

;

.

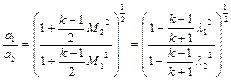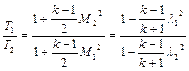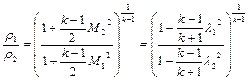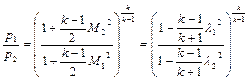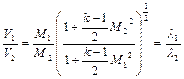Истинное давление, которое получается при торможении струи газа, может существенно отличаться от полного давления, определяемого формулой (2.7). Объясняется это тем, что в действительности торможение струи часто протекает не по идеальной адиабате, а с более или менее существенными гидравлическими потерями. Например, в диффузоре при дозвуковом течении газа уменьшение скорости обычно сопровождается вихреобразованиями, вносящими значительное сопротивления в газовый поток.

При торможении сверхзвукового потока почти всегда образуются ударные волны, дающие специфические «волновые» сопротивления.

Поэтому действительное давление в заторможенной струе газа (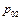) обычно ниже полного давления набегающей струи ().

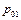Снижение давления оценивается коэффициентом сохранения полного давления

.

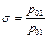Чем ниже 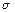, тем больше потери.

Итак, предельное значение скорости, выше которого нельзя применять формулы (2.7) при торможении газового потока, равно скорости звука ().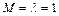

Для ускоряющегося газового потока этими формулами можно пользоваться и при сверхзвуковых скоростях, так как увеличение скорости происходит обычно без заметных потерь (изоэнтрпически) не только в области М < 1, но и в области М > 1, т.е. полное давление в ускоряющейся газовой струе почти не меняется. В частности, по формуле (2.7) вычисляют скорость истечение газа через сопло. При этом в баке, где газ покоится, давление равно полному давлению вытекающей струи 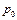, а в выходном отверстии сопла – статическому давлению .

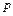В газовой динамике используют понятие энтропии, характеризующей состояние газа. Энтропия может быть представлена в виде дифференциального уравнения

,

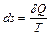где 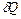– элементарное количество удельной теплоты (теплоты, отнесенное к единице массы газа).

В соответствии с первым законом термодинамики элементарное количество удельной теплоты равно

,

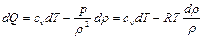откуда

.

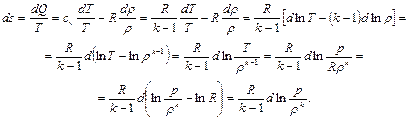Проинтегрировав последнее выражение, получим разность значений энтропии

.

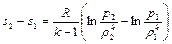В идеальном адиабатическом процессе

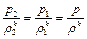
и изменение энтропии равно нулю.

Изменение энтропии можно представить в виде

.

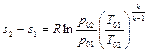Температура заторможенного газа характеризует собой полную энергию, которая в случае изолированной системы во всех сечениях одинакова, следовательно, 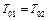. Поэтому уравнения для разности энтропий будет иметь вид

.

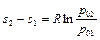Если в потоке нет потерь, то давление торможения постоянно, т.е. 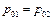, и изменение энтропии отсутствует. Процесс, при котором энтропия газа остается неизменной, называется изэнтропическим.

Адиабатический процесс в идеальном газе – изэнтропический.

При наличии потерь в потоке 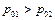, поэтому 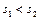, т.е. энтропия возрастает.

Процессы, происходящие с реальными газами, в изолированной системе приводят к увеличению энтропии.