В первую очередь рассмотрим задачу Коши дляоднородного уравнения теплопроводности.
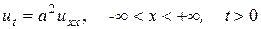 , (125)
, (125)
удовлетворяющее неоднородному начальному условию
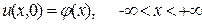 . (126)
. (126)
Начнем с того, что заменим переменные x и t на 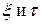 и введем в рассмотрение функцию
и введем в рассмотрение функцию 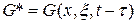 . Тогда функции
. Тогда функции 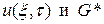 будут удовлетворять уравнениям
будут удовлетворять уравнениям
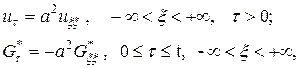
где 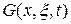 - функция Грина, определяемая формулой
- функция Грина, определяемая формулой
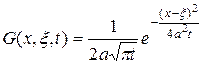 , (127)
, (127)
и обладающая свойствами
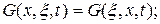 (128)
(128)
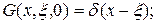 (129)
(129)
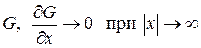 ; (130)
; (130)
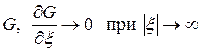 . (131)
. (131)
Умножив первое уравнение на G*, а второе на и и затем сложив полученные результаты, получим равенство
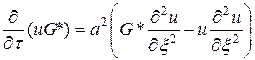 . (132)
. (132)
После интегрирования по частям равенства (132) по 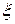 в пределах от -∞ до +∞ и по
в пределах от -∞ до +∞ и по 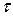 в пределах от 0 до t, получим
в пределах от 0 до t, получим
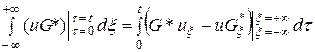 . (133)
. (133)
Если предполагать, что функция 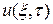 и ее производная
и ее производная 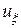 ограничены при
ограничены при 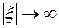 , то в силу свойств (131) интеграл в правой части (133) равен нулю. Следовательно, можно записать
, то в силу свойств (131) интеграл в правой части (133) равен нулю. Следовательно, можно записать
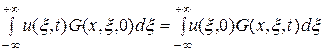 . (134)
. (134)
Заменив в этом равенстве 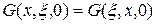 на
на 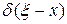 , а
, а 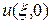 на
на 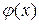 , получим соотношение
, получим соотношение
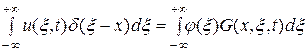
или
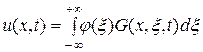 .
.
Отсюда, используя формулу (127) окончательно получим
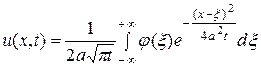 . (135)
. (135)
Формула (135) называется формулой Пуассона и определяет решение задачи Коши (125), (126) для однородного уравнения теплопроводности с неоднородным начальным условием.
Решение же задачи Коши для неоднородного уравнения теплопроводности
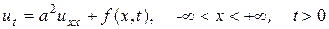 , (136)
, (136)
удовлетворяющее неоднородному начальному условию
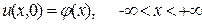 , (137)
, (137)
представляет собой сумму решений:
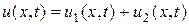 ,
,
где 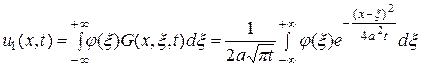 является решением задачи Коши для однородного уравнения теплопроводности.
является решением задачи Коши для однородного уравнения теплопроводности. 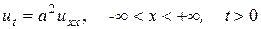 , удовлетворяющее неоднородному начальному условию
, удовлетворяющее неоднородному начальному условию 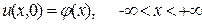 , а
, а 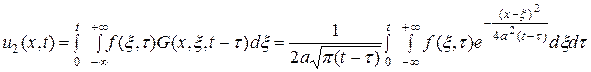 является решением
является решением 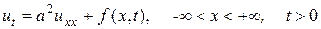 , удовлетворяющее однородному начальному условию
, удовлетворяющее однородному начальному условию 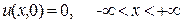 . Таким образом, решение задачи Коши (136), (137) определяется формулой
. Таким образом, решение задачи Коши (136), (137) определяется формулой
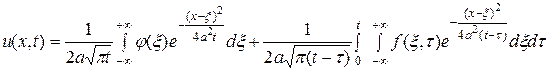 .(138)
.(138)
Пример 15. Найти решение уравнения
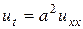 (15.1)
(15.1)
для следующего распределения температуры стержня:
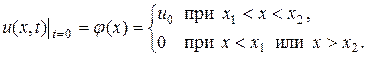 (15.2)
(15.2)
▲ Стержень является бесконечным, поэтому решение можно записать, используя формулу (135)
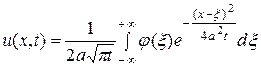 .
.
Так как 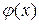 в интервале
в интервале 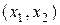 равна постоянной температуре
равна постоянной температуре 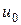 , а вне этого интервала температура равна нулю, то решение принимает вид
, а вне этого интервала температура равна нулю, то решение принимает вид
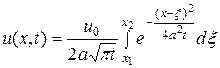 . (15.3)
. (15.3)
Полагая в (15.3) 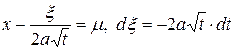 , получим
, получим
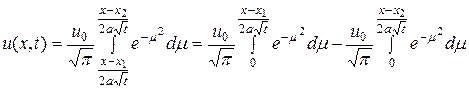 .
.
Поскольку
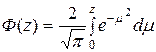
представляет собой интеграл вероятностей, то окончательное решение исходной задачи (13.1), (13.2) можно выразить формулой
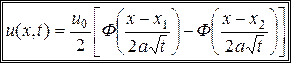 .▲
.▲
 2015-01-30
2015-01-30 5472
5472
