Задача Коши для уравнения теплопроводности имеет вид
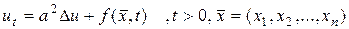 (139)
(139)
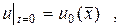 (140)
(140)
где 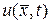 – неизвестная функция,
– неизвестная функция, 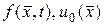 – заданы.
– заданы.
Разложим функцию 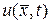 при любом фиксированном
при любом фиксированном 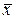 в ряд Тейлора по времени относительно точки t =0 (ряд Маклорена)
в ряд Тейлора по времени относительно точки t =0 (ряд Маклорена)
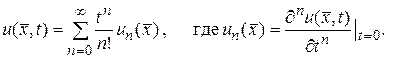
 (141)
(141)
Если найти коэффициенты 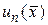 , то по формуле (141) получим решение. Заметим, что
, то по формуле (141) получим решение. Заметим, что 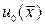 определяется из начального условия (140).
определяется из начального условия (140).
Разложим в ряд Маклорена функцию 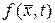 в правой части уравнения (139)
в правой части уравнения (139)
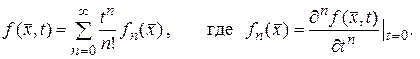 (142)
(142)
Поскольку функция 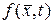 задана, то все
задана, то все 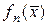 могут быть найдены.
могут быть найдены.
Выражения для частной производной 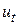 и оператора Лапласа
и оператора Лапласа 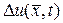 в уравнении (139), следуют из (141)
в уравнении (139), следуют из (141)
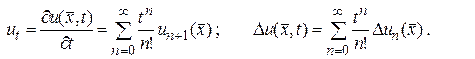 (143)
(143)
Подставим (142) и (143) в уравнение (139). В результате получим равенство
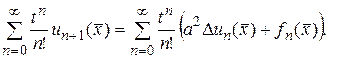
Это равенство равносильно соотношениям
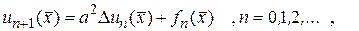 (144)
(144)
которые определяют коэффициенты 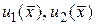 и так далее через
и так далее через 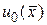 , заданную в начальном условии (140).
, заданную в начальном условии (140).
Таким образом, решение задачи Коши (139)–(140) выражается формулой:
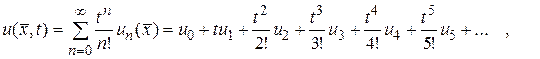 (145)
(145)
где 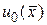 задана в (140), а остальные
задана в (140), а остальные 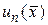 находятся по (144)
находятся по (144)
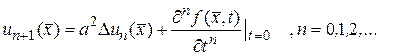 (146)
(146)
Пример 16. Найти решение уравнения
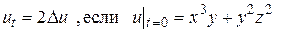
▲ Здесь 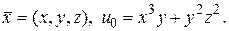 Так как
Так как 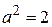 и
и 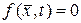 , то по (146)
, то по (146) 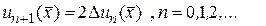 Отсюда находим
Отсюда находим
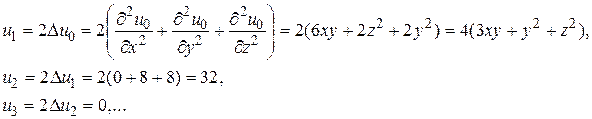
То есть, все остальные 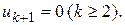
Подставляем полученные 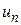 в решение (145)
в решение (145)
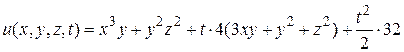
или
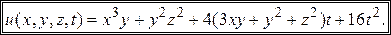 ▲
▲
Пример 17. Найти решение уравнения
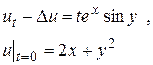
▲ Здесь 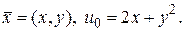 Так как
Так как 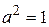 и
и 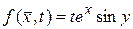 , то по (146)
, то по (146)
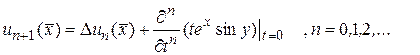
Найдем 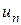 по этой формуле
по этой формуле
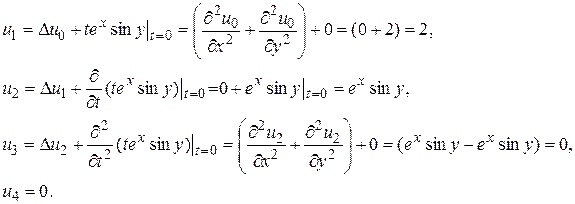
И так далее, все остальные 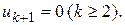
Подставляем полученные 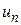 в решение (145)
в решение (145)
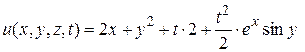
или
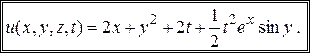 ▲
▲
 2015-01-30
2015-01-30 1500
1500
