Прямоугольную систему координат обозначают 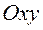 , а плоскость, в которой расположена система координат, называют координатной плоскостью.
, а плоскость, в которой расположена система координат, называют координатной плоскостью.
Рассмотрим произвольную точку М плоскости 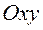 . Вектор
. Вектор 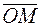 называется радиусом-вектором точки М.
называется радиусом-вектором точки М.
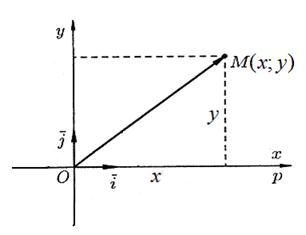
Координатами точки М в системе координат 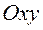 называются координаты радиуса-вектора
называются координаты радиуса-вектора 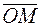 . Если
. Если 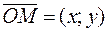 , то координаты точки М записывают так: М(х;у), число х называется абсциссой точки М, у — ординатой точки М.
, то координаты точки М записывают так: М(х;у), число х называется абсциссой точки М, у — ординатой точки М.
Эти два числа х и у полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором 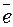 того же направления, что и луч Ор.
того же направления, что и луч Ор.
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием 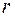 от полюса О и
от полюса О и 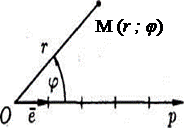 углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой
углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой
Рис. 1 стрелки) (рис. 1).
Числа r и φ называются полярными координатами точки М, пишут 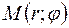 , при этом r называют полярным радиусом, φ — полярным углом.
, при этом r называют полярным радиусом, φ — полярным углом.
Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком 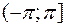 (или
(или 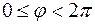 ), а полярный радиус —
), а полярный радиус — 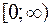 . В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, иобратно.
. В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, иобратно.
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы 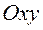 , а полярную ось — с положительной полуосью Ох. Пусть х и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.
, а полярную ось — с положительной полуосью Ох. Пусть х и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.
Из рисунка 2 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
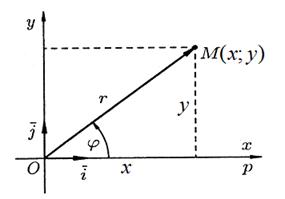 . Рис 2. . Рис 2. | 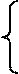 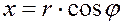 , , 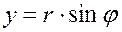 . Полярные же координаты точки М выражаются через декартовы координаты (тот же рисунок) такими формулами: . Полярные же координаты точки М выражаются через декартовы координаты (тот же рисунок) такими формулами: |

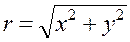 ,
,
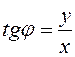 .
.
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что 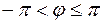 .
.
2. Основные приложения метода координат на плоскости.
 2014-10-30
2014-10-30 748
748








