2014-10-30
449
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N (0; b) пересечения с осью Оу и углом α между осью Ох и прямой (рис. 13). Под углом α (0 ≤ α < π) наклона прямой понимается наименьший угол, на который нужно повернуть против часовой стрелки ось Ох до ее совпадения с прямой.
Рис. 13
Из определения тангенса угла следует равенство 
,
т. е.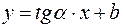 
. Введем обозначение 
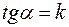, получаем уравнение
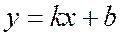. (4)
Число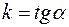 
называется угловым коэффициентом прямой, а уравнение (4) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид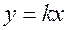 
.
Если прямая параллельна оси Ох, то α = 0, следовательно,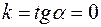 
и уравнение (4) примет вид у = b.
Если прямая параллельна оси Оу, то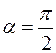 
, уравнение (4) теряет смысл, т. к. для нее угловой коэффициент 
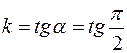не существует. В этом случае уравнение прямой будет иметь вид
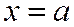, (5)
где а — абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (4) и (5) есть уравнения первой степени.
