2014-10-30
490
Найдем уравнение прямой, проходящей через заданную точку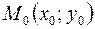 
перпендикулярно данному ненулевому вектору 
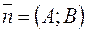. Возьмем на прямой произвольную точку 
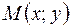) и рассмотрим вектор 
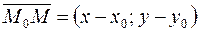(рис. 15).
Рис. 15
Поскольку векторы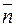 
и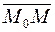 
перпендикулярны, то их скалярное произведение равно нулю: 
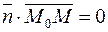, то есть
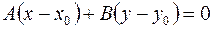. (11)
Уравнение (11) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Как было отмечено выше, вектор 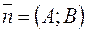, перпендикулярный прямой, называется нормальным вектором этой прямой.
Уравнение (11) можно переписать в виде
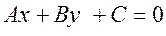, (12)
где А и В — координаты нормального вектора, С = – Ax0 – By0 — свободный член. Уравнение (12) есть общее уравнение прямой.
