Расстояние от точки до прямой. Пусть заданы прямая уравнени­ем и точка (рис

Пусть заданы прямая 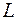уравнени­ем 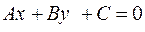и точка 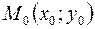(рис. 17). Требуется найти расстояние от точки 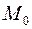до прямой .

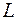· Решение: Расстояние 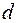от точки 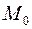до прямой 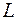равно модулю проекции вектора 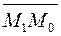, где 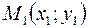— произвольная точ­ка прямой 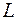, на направление нормального вектора 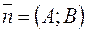. Следовательно,

.

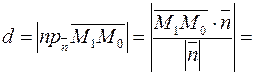
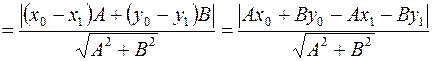Так как точка 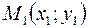принадлежит прямой , то 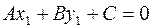, т. е. 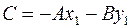. Поэтому

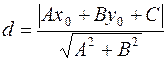, (15)

что и требовалось получить.

Пример. Найти расстояние от точки 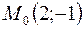до прямой

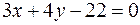
· Решение: По формуле (14) получаем

.

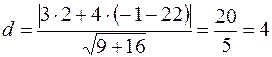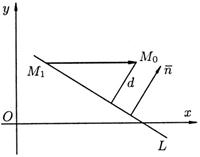
Рис. 17