Пусть на 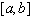 задана последовательность сеток
задана последовательность сеток 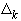 :
: 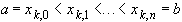 ,
, 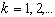 , которая удовлетворяют условию
, которая удовлетворяют условию 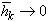 при
при 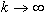 . Для
. Для 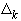 строится интерполяционный сплайн
строится интерполяционный сплайн 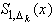 . Интерполяционный процесс сходится, если
. Интерполяционный процесс сходится, если
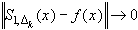 при
при 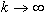 для любой функции
для любой функции 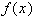 из некоторого класса. Отсюда вытекает возможность интерполяции с наперед заданной точностью:
из некоторого класса. Отсюда вытекает возможность интерполяции с наперед заданной точностью:
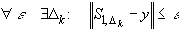 .
.
Преимущество по сравнению с интерполяционными многочленами: из оценки погрешности следует сходимость.
Пусть 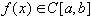 . По доказанной теореме
. По доказанной теореме 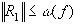 .
.
По определению 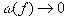 при
при 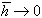 , поэтому процесс интерполяции линейными сплайнами сходится на множестве непрерывных функций по произвольной последовательности сеток
, поэтому процесс интерполяции линейными сплайнами сходится на множестве непрерывных функций по произвольной последовательности сеток 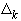 .
.
Если 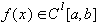 ,
, 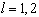 , то
, то 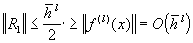 . Сходимость порядка
. Сходимость порядка 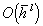 .
.
 2015-01-30
2015-01-30 282
282








