Вопросы и задачи. п1. В треугольнике АВС сторона АВ разделена точками М и N на три равные части

п1. В треугольнике АВС сторона АВ разделена точками М и N на три равные части. Найти вектор 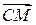, если .

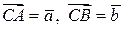п2. Дано: 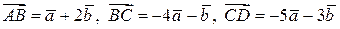. Доказать, что ABCD – трапеция. (Указание: найти вектор 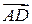и доказать, что )

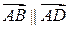п3. Даны точки: А(0;2;3), В(-1;2;5), С(4;-2;-3).

а) Найти координаты векторов .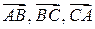

б) Найти координаты точки D, так, чтобы четырехугольник ABCD был параллелограммом

п4. Найти скалярное произведение векторов 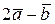и 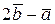, если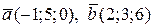

п5. Даны 2 вектора: 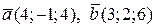. Будучи отложены из одной точки, они образуют две стороны треугольника. Найти:

а) длины сторон этого треугольника, б) углы этого треугольника

п6. Найти векторное произведение векторов 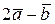и 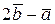, если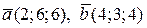

п7. Найти площадь треугольника из задачи п5.

п8. Пусть даны два вектора на плоскости: .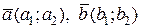

а) запишите в координатном выражении условие коллинеарности (параллельности) этих векторов.

б) запишите в координатном выражении условие перпендиклярности этих векторов.

в) существует ли векторное произведение этих векторов? (если да – найдите, если нет – объясните)