Действия над комплексными числами в показательной форме выполняются по правилам действий со степенями:
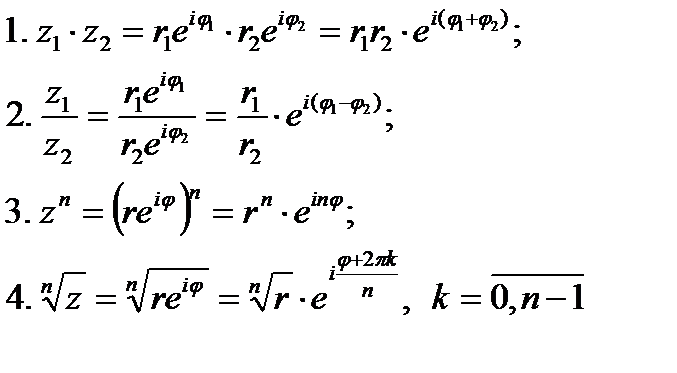
Решение уравнений с помощью комплексных чисел .
1. Решить квадратное уравнение 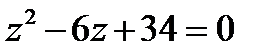 .
.
Решение.
Вычислим дискриминант: 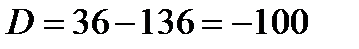
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах:
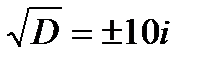
По известным школьным формулам получаем два корня:
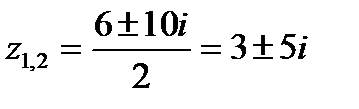 – сопряженные комплексные корни.
– сопряженные комплексные корни.
2. Найти действительные x и y из уравнения: 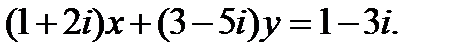
Решение.
В левой части уравнения раскроем скобки и сгруппируем действительные и мнимые слагаемые:
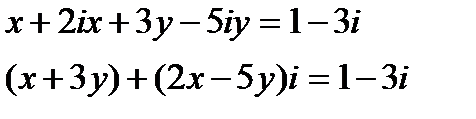
Воспользуемся условием равенства комплексных чисел:
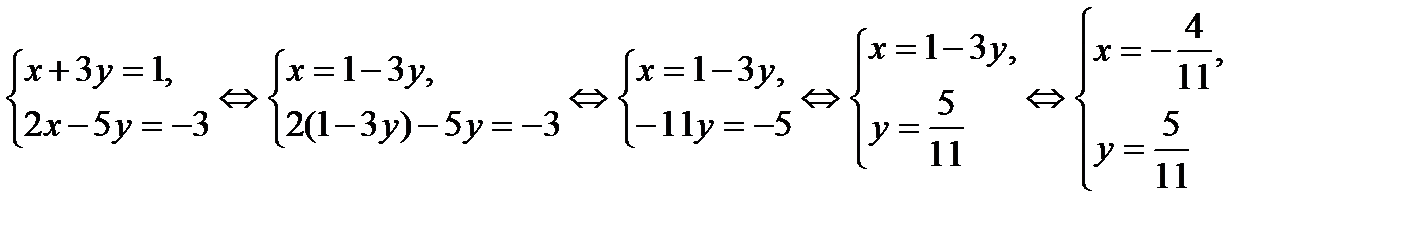
 2015-01-30
2015-01-30 10628
10628
