Действия над комплексными числами в тригонометрической форме

Числа в тригонометрической форме не складывают и не вычитают.

Пусть z₁ = r₁(cos φ₁ + i sin φ₁) и z₂=r₂(cos φ₂ + i sin φ₂).

1. Произведение комплексных чисел вычисляется по формуле:

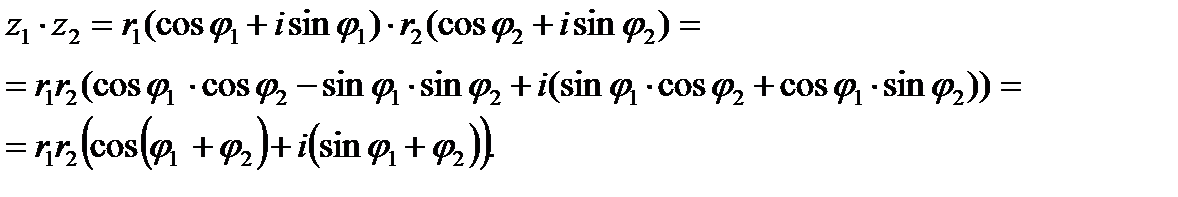
Пример. Найти произведение комплексных чисел

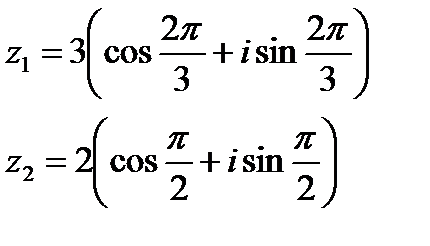
Решение:

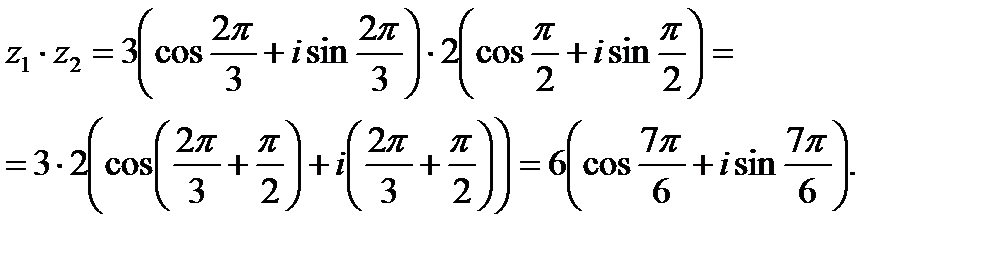
2. Частное комплексных чисел вычисляется по формуле:

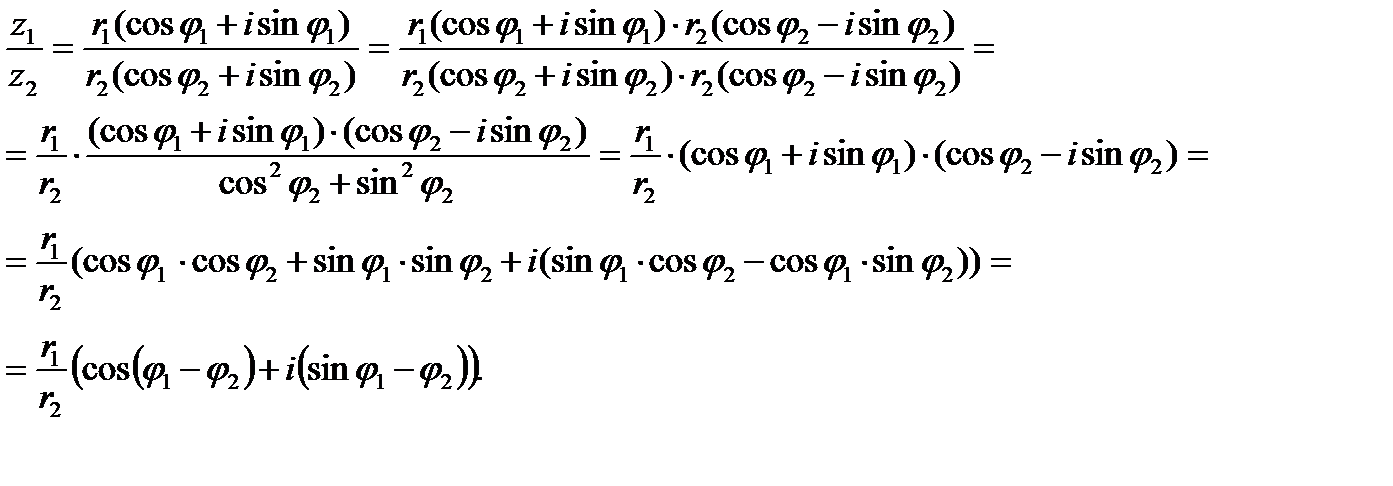
Пример. Выполнить деление комплексных чисел.

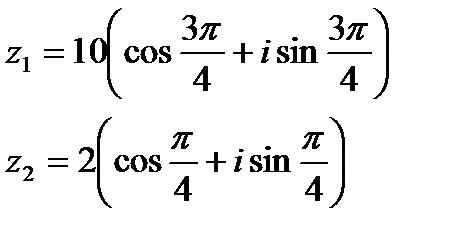
Решение:

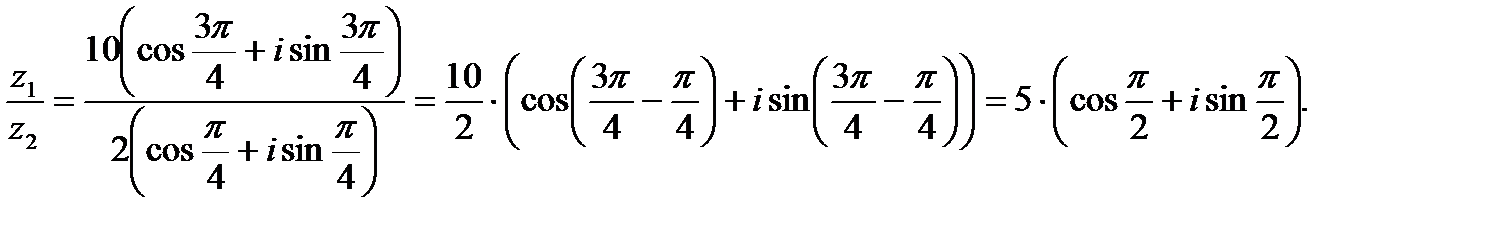
Т.е. в тригонометрической форме операции умножения и деления производятся следующим образом: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.

Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ₁, φ₂,..., φ_n – аргументы чисел z₁, z₂,..., z_n, то

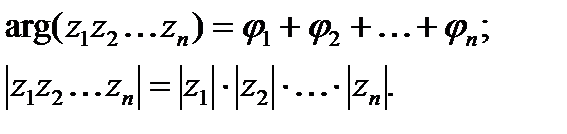
3. В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

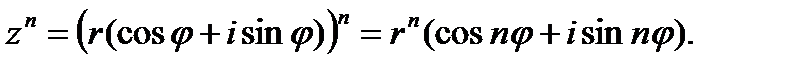Первая формула Муавра.

Пример

Дано комплексное число 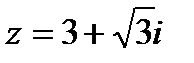, найти .

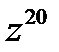Решение:

Сначала нужно представить данное число в тригонометрической форме.

Найдём модуль этого числа: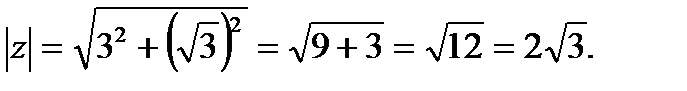

Аргумент данного числа находится из системы:

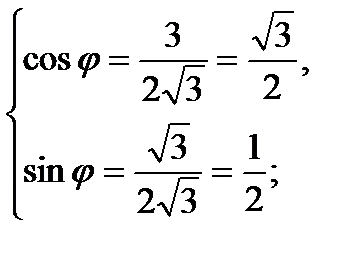
Значит, один из аргументов числа 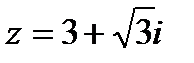равен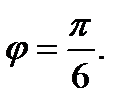

Получаем:

.

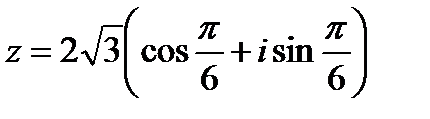Тогда, по формуле Муавра:

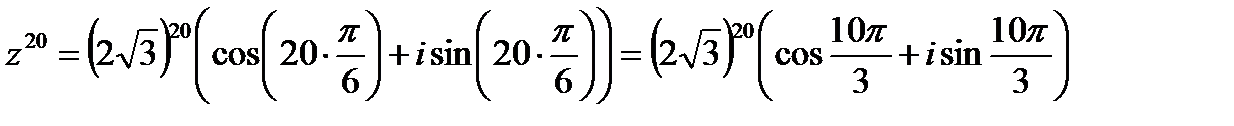
Считать на калькуляторе 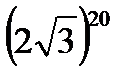не нужно, а вот угол в большинстве случае следует упростить. Как упростить? Нужно избавиться от лишних оборотов. Один оборот составляет 2p радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе 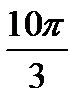.Для удобства делаем дробь правильной: 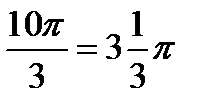, после чего становится хорошо видно, что можно убавить один оборот: 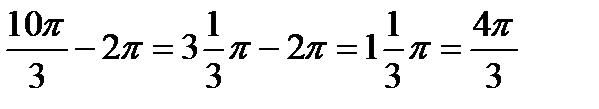. Таким образом, окончательный ответ запишется так: .

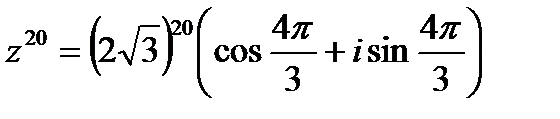Можно убавить еще один оборот и получить главное значение аргумента:

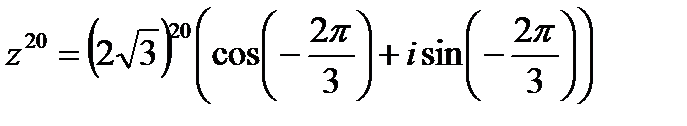
4. Для извлечения корня n -й степени из комплексного числа 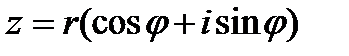используется вторая формула Муавра:

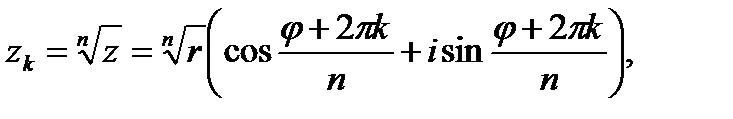
где 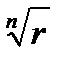- арифметический корень из модуля комплексного числа, k =0, 1, 2,…, n -1