Докажем предварительно две леммы.
Лемма 1.1. Через любые три точки М1 (х1; у1), М2 (х2; у2), М3 (х3; у3) с различными абсциссами можно провести единственную кривую вида
у=Ах2+Вх+С (1)
Доказательство. Подставляя в уравнение параболы (1) координаты точек М1, М2 , М3 , получаем систему трех уравнений первой степени с тремя неизвестными А, В, С:
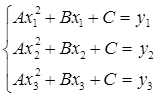
Так как числа х1, х2, х3 различны, то определитель этой системы отличен от нуля:
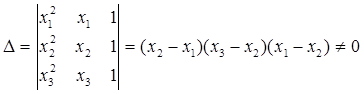
Следовательно, данная система имеет единственное решение, т.е. коэффициенты А, В, С определяются однозначно. g
Отметим, что если А¹0, то кривая (1) является параболой, если А=0, то прямой.
Лемма 1.2. Площадь s криволинейной трапеции, ограниченной кривой у=Ах2+Вх+С, проходящей через точки М1 (-h; y1), M2 (0, y2), M3 (h, y3) (рис. 2) выражается формулой
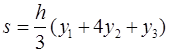 (2)
(2)
Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что
2Аh2+2С=у1+у3; С=у2 (3)
Учитывая соотношение (3), имеем
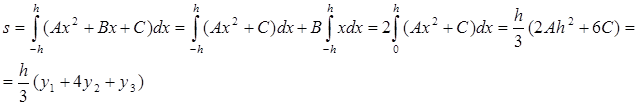
Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0<x1<x2<...<x2k<x2k+1<x2k+2<...<x2n-1<x2n=b, а кривую y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками М0, М1 , М2 ,..., М2k, М2k+1, М2k+2,..., М2n-2, М2n-1, М2n (рис. 3).
Через каждую тройку точек
М0 М1 М2 ,..., М2k М2k+1 М2k+2,..., М2n-2 М2n-1 М2n
проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)]
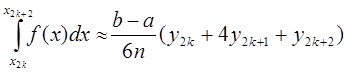
где yk=f(xk), k=0, 1, 2,...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу
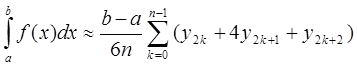
или в развернутом виде
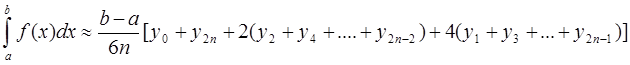
Эта формула называется формулой парабол или формулой Симпсона.
В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3,..., х2n-1 имеет коэффициент 4, в четных точках х2, х4,..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, х1, х2n =b - коэффициент 1.
Геометрический смысл формулы Симпсона очевиден: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами (прямыми).
В полных курсах высшей математики доказывается, что если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем
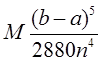
где М - наибольшее значение 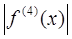 на отрезке [a, b]. Выше отмечалось, что погрешность формулы трапеций оценивается числом
на отрезке [a, b]. Выше отмечалось, что погрешность формулы трапеций оценивается числом
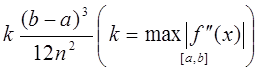
Так как n4 растет быстрее, чем n2, то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций. Этим и объясняется, что формула Симпсона позволяет получить большую точность, чем формула трапеций.
Для сравнения точности приближенных формул вычислим еще раз интеграл
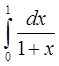 , но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.
, но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.
По формуле Симпсона получаем
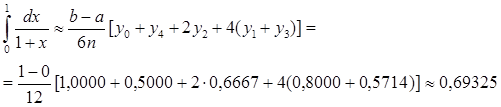
Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f(4)(x)=24/(1+x)5, откуда следует, что на отрезке [0, 1] 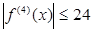 . Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 44),0б0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.
. Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 44),0б0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.
Как отмечалось выше, приближенные формулы для вычисления определенного интеграла применяют в тех случаях, когда первообразная подынтегральной функции не выражается через элементарные функции.
Вычислим, например, интеграл 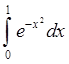 по формуле Симпсона с точностью до 0,001.
по формуле Симпсона с точностью до 0,001.
Чтобы выбрать необходимое для получения заданной точности число 2n, найдем f(4)(x). Последовательно дифференцируя функцию f(x)= 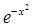 , получаем
, получаем
f(4)(x)=4 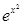 (4х4-12х2+3)
(4х4-12х2+3)
Так как на отрезке [0, 1] 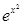 £1, ½4х4-12х2+3½£5, то
£1, ½4х4-12х2+3½£5, то 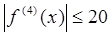 . Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем 20/2880n4<1/1000, откуда n4 >1000/144. Для того чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.
. Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем 20/2880n4<1/1000, откуда n4 >1000/144. Для того чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.
Разобьем теперь отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)= 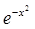 в этих точках у0=1,0000, у1=0,9394, у2=0,7788, у3=0,5698, у4=0,3679. Применяя формулу Симпсона, получаем
в этих точках у0=1,0000, у1=0,9394, у2=0,7788, у3=0,5698, у4=0,3679. Применяя формулу Симпсона, получаем
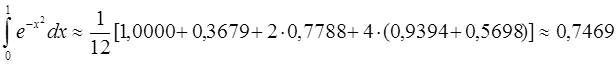
Таким образом, 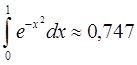 с точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и заменив рассматриваемый интеграл суммой, стоящей в правой части формулы Симпсона, мы вычислили данный интеграл с необходимой точностью.
с точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и заменив рассматриваемый интеграл суммой, стоящей в правой части формулы Симпсона, мы вычислили данный интеграл с необходимой точностью.
В заключении отметим, что каждый из изложенных методов приближенного вычисления интегралов содержит четкий алгоритм их нахождения, что позволяет широко применять эти методы для вычислений на ЭВМ. Таким образом, указанные методы - эффективное средство вычисления интегралов. Для интегралов, которые нельзя выразить через элементарные функции, с помощью ЭВМ и простейших приближенных методов можно составить таблицы их значений.
Основные понятия о дифференциальных уравнениях. Дифференциальные уравнения 1-го порядка. Теорема о существовании и единственности решения задачи Коши. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальным уравнением называется уравнение вида 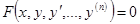 , где
, где 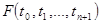 - функция, определенная в некоторой области
- функция, определенная в некоторой области 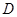 пространства
пространства 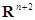 ,
, 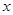 - независимая переменная,
- независимая переменная, 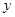 - функция от
- функция от 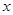 ,
, 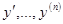 - ее производные.
- ее производные.
Порядком уравнения называется наивысший из порядков производных 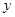 , входящих в уравнение.
, входящих в уравнение.
Функция 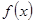 называется Решением уравнения на промежутке
называется Решением уравнения на промежутке 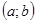 , если для всех
, если для всех 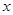 из
из 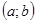 выполняется равенство:
выполняется равенство: 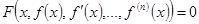 .
.
Интегральная кривая – это график решения.
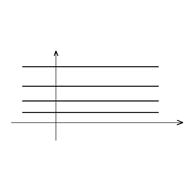
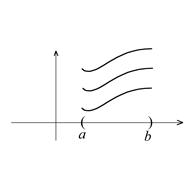
Пример 1. Решить уравнение 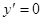 . Его решение:
. Его решение: 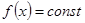 определено на
определено на 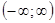 . Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
. Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
 |  |
Пример 2. Решить уравнение 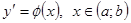 , где
, где 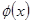 - непрерывная на
- непрерывная на 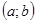 функция. Пусть
функция. Пусть 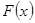 - первообразная для
- первообразная для 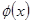 . Тогда уравнение имеет бесконечное множество решений на
. Тогда уравнение имеет бесконечное множество решений на 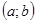 и все они имеют вид
и все они имеют вид 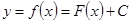 , где
, где 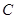 - произвольная постоянная.
- произвольная постоянная.
Есть прямой способ выбрать какое-то одно из этих решений, потребовав, например, чтобы для некоторой точки 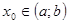 выполнялось условие
выполнялось условие 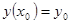 . Тогда, подставив
. Тогда, подставив 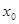 в решение, получаем условие
в решение, получаем условие 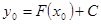 , определяющее
, определяющее 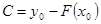 и, тем самым, единственное решение
и, тем самым, единственное решение 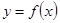 с указанным условием.
с указанным условием.
Рассмотрим значительно более общую ситуацию, чем была в примерах. Пусть исследуемое уравнение имеет вид: 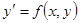 . Это – уравнение первого порядка, Разрешенное Относительно
. Это – уравнение первого порядка, Разрешенное Относительно 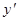 . (Термин «разрешенное» означает, что
. (Термин «разрешенное» означает, что 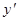 выражается через остальные величины, в отличие от уравнения общего вида
выражается через остальные величины, в отличие от уравнения общего вида 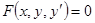 , из которого выразить
, из которого выразить 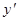 может быть и не удастся).
может быть и не удастся).
Сформулируем важнейшую теорему.
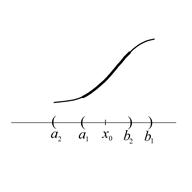
Теорема. (О существовании и единственности решения задачи Коши). Пусть 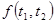 - непрерывная функция в области
- непрерывная функция в области 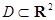 , причем
, причем 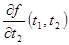 - также непрерывен в
- также непрерывен в 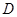 . Тогда для любой точки
. Тогда для любой точки 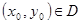 Задача Коши:
Задача Коши: 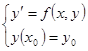 имеет решение, причем единственное в том смысле, что если есть 2 ее решения
имеет решение, причем единственное в том смысле, что если есть 2 ее решения 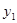 и
и 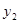 , определенные на интервалах
, определенные на интервалах 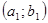 и
и 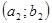 , содержащих точку
, содержащих точку 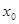 , то они совпадают на пересечении
, то они совпадают на пересечении 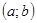 этих интервалов.
этих интервалов.
Теорему оставим Без доказательства.
Замечание. Говорят, что решение 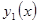 дифференциального уравнения на интервале
дифференциального уравнения на интервале 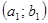 есть Продолжение решения
есть Продолжение решения 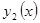 на
на 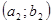 , если
, если 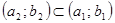 и
и 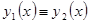 на
на 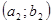 . Также говорят, что решение
. Также говорят, что решение 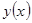 - Максимальное или Непродолжаемое относительно
- Максимальное или Непродолжаемое относительно 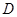 , если
, если 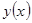 не обладает продолжениями, целиком лежащими в
не обладает продолжениями, целиком лежащими в 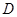 .
.
На основании этого замечания можно сказать, что при условиях теоремы существует единственное максимальное (непродолжаемое) решение задачи Коши.
Геометрический смысл сформулированной теоремы состоит в следующем. Левая часть уравнения 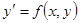 представляет собой
представляет собой 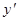 - тангенс угла наклона касательной к графику искомой функции в точке
- тангенс угла наклона касательной к графику искомой функции в точке 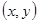 , а правая часть
, а правая часть 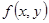 задает его численное значение
задает его численное значение 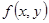 в этой точке. Поэтому можно считать, что уравнение задает Поле направлений на области
в этой точке. Поэтому можно считать, что уравнение задает Поле направлений на области 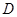 , т. е. к каждой точке
, т. е. к каждой точке 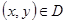 прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.
прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.

Поэтому сформулированная выше теорема означает, что при выполнении ее условий через каждую точку 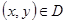 проходит единственная непродолжаемая интегральная кривая.
проходит единственная непродолжаемая интегральная кривая.
Перейдем к простейшим типам дифференциальных уравнений, для которых можно в явном виде получить их решения.
Уравнения с разделяющимися переменными. Уравнениями с разделяющимися переменными называются уравнения вида 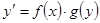 , где
, где 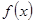 - непрерывна на некотором
- непрерывна на некотором 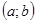 , а
, а 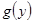 непрерывна на
непрерывна на 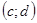 , причем
, причем 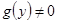 на
на 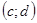 .
. 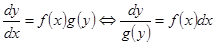 . Интегрируя обе части, получаем
. Интегрируя обе части, получаем 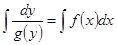 . Обозначая
. Обозначая 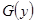 любую первообразную для
любую первообразную для 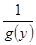 , а
, а 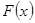 - любую первообразную для
- любую первообразную для 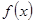 , перепишем это уравнение в виде
, перепишем это уравнение в виде 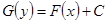 . Это – искомая интегральная кривая.
. Это – искомая интегральная кривая.
Рассмотрим некоторые примеры таких уравнений.
Пример 1. 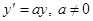 . Очевидно решение
. Очевидно решение 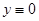 . Если же
. Если же 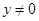 , то уравнение можно заменить таким:
, то уравнение можно заменить таким: 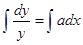 , откуда
, откуда 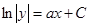 . Если считать, что
. Если считать, что 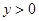 , то
, то 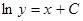 , откуда
, откуда 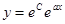 или
или 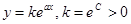 . Аналогично, при
. Аналогично, при 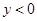 получаем
получаем 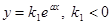 .
.
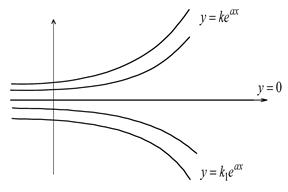
Пример 2. 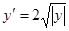 .
. 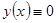 - решение уравнения. При
- решение уравнения. При 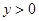 имеем:
имеем: 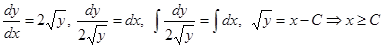 , и
, и 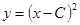 . Аналогично, при
. Аналогично, при 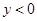
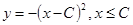 .
.
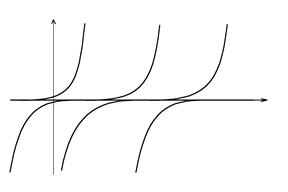
В точках 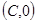 единственность решения нарушается. Отметим, что это не противоречит теореме единственности:
единственность решения нарушается. Отметим, что это не противоречит теореме единственности: 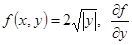 - не непрерывен в 0.
- не непрерывен в 0.
Однородные уравнения. Под Однородными уравнениями понимаются уравнения вида 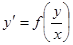 . Для их решения требуется сделать замену
. Для их решения требуется сделать замену 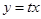 , после чего получится уравнение с разделяющимися переменными.
, после чего получится уравнение с разделяющимися переменными.
Пример. 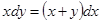 . Оно имеет решение
. Оно имеет решение 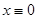 . Пусть теперь
. Пусть теперь 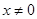 . Преобразуем уравнение так:
. Преобразуем уравнение так: 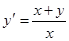 (правая часть имеет вид
(правая часть имеет вид 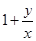 - это однородное уравнение). Полагаем
- это однородное уравнение). Полагаем 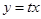 . При этом
. При этом 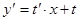 и получаем уравнение
и получаем уравнение 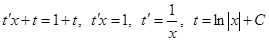 . Значит,
. Значит, 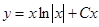 .
.
Уравнения вида 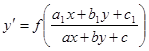 . Такие уравнения сводятся к однородным заменой переменных. В случае, если прямые
. Такие уравнения сводятся к однородным заменой переменных. В случае, если прямые 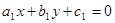 и
и 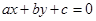 пересекаются в точке
пересекаются в точке 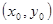 , то замена
, то замена 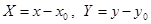 приведет уравнение к однородному. Если же эти прямые не пересекаются, то
приведет уравнение к однородному. Если же эти прямые не пересекаются, то 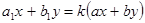 и замена
и замена 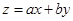 приведет к уравнению с разделяющимися переменными.
приведет к уравнению с разделяющимися переменными.
 2015-01-07
2015-01-07 2358
2358
