Выборочным корреляционным отношением

Y к Х называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Y:

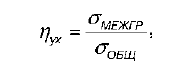
где Gмежгр – это межгрупповое среднее квадратическое отклонение переменной Y:

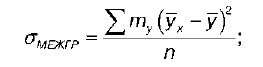
G общ – это общее среднее квадратическое отклонение переменной Y:

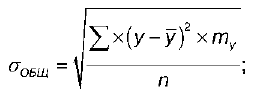
где n – объем выборки (сумма всех частот);

m х – частота значениях переменной X;

m – частота значения у переменной Y;

у – среднее значение переменной Y;

у х – условная средняя переменной Y.

Выборочным корреляционным отношением X

к Y называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Х:

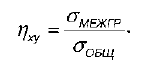
Выборочное корреляционное отношение обладает следующими свойствами:

1) значение выборочного корреляционного отношения принадлежит интервалу от нуля до единицы включительно:

0 ≤ η yx ≤ 1;

2) если η yx = 0, т. е. значение выборочного корреляционного отношения равно нулю, то между исследуемыми переменными Y и Х корреляционная зависимость отсутствует; 3) если η yx = 1, т. е. значение выборочного корреляционного отношения равно единице, то между исследуемыми переменными Y и Х существует функциональная зависимость;

4) выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции:

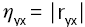
5) если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, т. е. если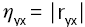

то между исследуемыми переменными существует точная линейная корреляционная зависимость. Основным достоинством выборочного корреляционного отношения η yx по сравнению с выборочным коэффициентом корреляции r yx является то, что показатель выборочного корреляционного отношения можно использовать как меру тесноты любой формы связи.