Выберем базисные функции в виде последовательности степеней аргумента x:
φ 0(x) = x 0 = 1; φ 1(x) = x 1 = x; φ m(x) = x m, m < n.
Расширенная матрица Грама для степенного базиса будет выглядеть следующим образом:
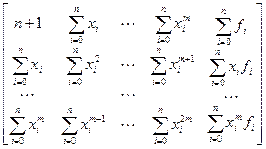 .
.
Особенность вычислений такой матрицы (для уменьшения количества выполняемых действий) состоит в том, что необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. В некоторых языках программирования, где отсутствует быстрая процедура возведения в степень, пригодится алгоритм расчета матрицы Грама, представленный далее.
Выбор базисных функций в виде степеней x не является оптимальным с точки зрения достижения наименьшей погрешности. Это является следствием неортогональности выбранных базисных функций. Свойство ортогональности заключается в том, что для каждого типа полинома существует отрезок [ x 0, x n], на котором обращаются в нуль скалярные произведения полиномов разного порядка:
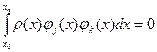 , j ≠ k, ρ – некоторая весовая функция.
, j ≠ k, ρ – некоторая весовая функция.
Если бы базисные функции были ортогональны, то все недиагональные элементы матрицы Грама были бы близки к нулю, что увеличило бы точность вычислений, в противном случае при 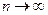 определитель матрицы Грама очень быстро стремится к нулю, т.е. система становится плохо обусловленной.
определитель матрицы Грама очень быстро стремится к нулю, т.е. система становится плохо обусловленной.
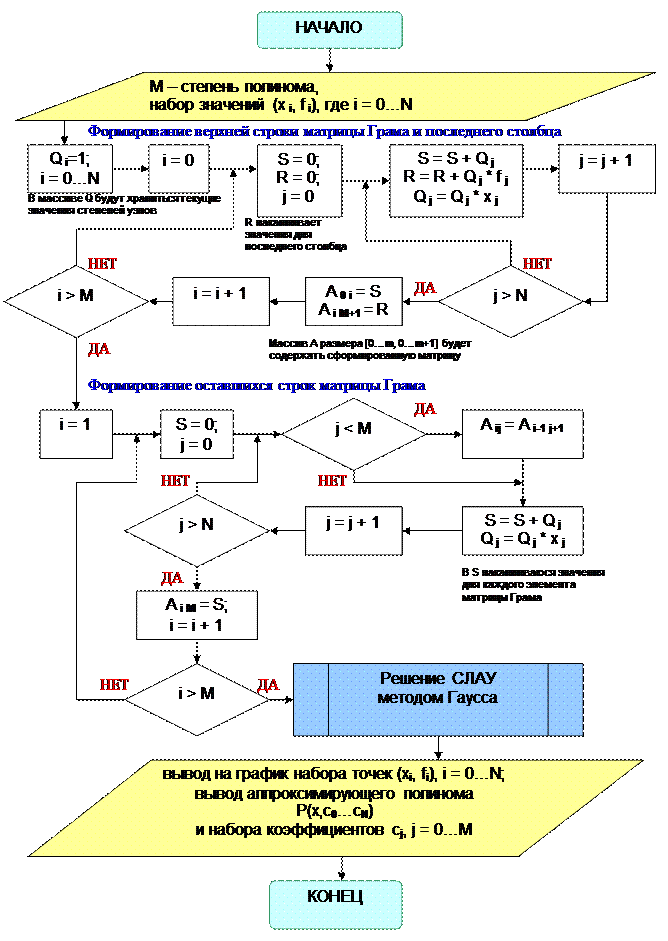
Блок-схема алгоритма формирования матрицы Грама и аппроксимации полиномом.
 2015-01-07
2015-01-07 799
799








