Пусть x 1 и x 2 (x 1 < x 2) — нули дифференцируемой функции y = f (x), т.е. f (x 1) = f (x 2) = 0.
Тогда на отрезке [ x 1, x 2] функция y = f (x) удовлетворяет условиям теоремы Ролля:
f (x) непрерывна на отрезке [ x 1, x 2], так как она дифференцируема на этом отрезке;
f (x) дифференцируема в интервале (x 1, x 2), так как она дифференцируема на отрезке [ x 1, x 2];
на концах отрезка [ x 1, x 2] f (x) принимает равные значения.
Следовательно, по теореме Ролля существует, по крайней мере, одна точка c Î (x 1, x 2), в которой f '(c) = 0.
30.Теоремы Лагранжа и Коши о дифференцируемых функциях.
Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [ а; b ] и дифференцируема в интервале (а; b), то в этом интервале найдется такая точка с, что 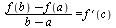
Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ. 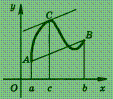
Следствие. Если f ′(x) = 0 в интервале (а; b), то в этом интервале функция f (х) постоянна.
Пример 13.2. На кривой 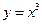 найти точку, в которой скорость изменения имеет среднее значение на отрезке
найти точку, в которой скорость изменения имеет среднее значение на отрезке 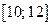 .
.
Решение. Запишем формулу Лагранжа с учетом, что 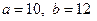 и
и 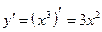 .
.
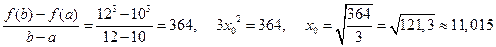 ,
,
т.е. близко к середине отрезка 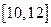 . Число 364 – это скорость. Она может измеряться в км/ч, если x измеряется в часах, y в километрах; руб./мес., если y – это деньги, x – время в месяцах и т.д.
. Число 364 – это скорость. Она может измеряться в км/ч, если x измеряется в часах, y в километрах; руб./мес., если y – это деньги, x – время в месяцах и т.д.
Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [ а; b ];
2) дифференцируемы в интервале (а; b);
3) g' (x) ≠ 0 в этом интервале,
то в интервале (а; b) существует такая точка с, что имеет место равенство
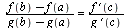
 2015-01-13
2015-01-13 1459
1459
