Биномиальное распределение. Распределение Пуассона

Определим ДСВ как число появления случ.события в n испытаниях по схеме Бернулли, т.е. вер-ть появления события в каждом испытании постоянно и=р и исходы испытаний не зависимы друг от друга. Возможные значения СВ х1=0, х2=1,…,хn+1=n. Вер-ти этих возможных значений вычисл-ся по формуле Бернулли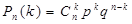

Распределение этой СВ в виде табл:

х			…	k	…	n
р	qn	npqn-1		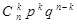		pn

Это распределение назыв-ся биномиальным, т.к. вер-ть возможного значения СВ(Х)=k=общему числу разложения бинома Ньютона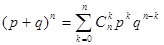

Найдем численные хар-ки биномиального распределения. Для этого рассмотрим х_i – число появления события в одном i-ом испытании. Ее распределение представлено табл.

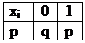М(Х)=0·q+1р=р

D(X_i)=M(X_i²)-M²(X_i)=0²·q+1²·р-р²=р-р²=р(1-р)=pq

Т.о. МО числа появляющегося события в единичном испытании=вер-ти его появления, а дисперсия – произведению вер-ти его появления на вер-ть непоявления.

СВ Х – число появления события в n испытании=сумме СВ х₁,…х_n:Х=Σх_i.

Пользуясь св-вами МО и дисперсии для суммы незав. СВ, имеем, что М(Х)=М(Σх_i)=ΣМ(х_i)=Σр=nр.

Дисперсия: D(Х)=D(Σх_i)=ΣD(х_i)=Σpq=npq

Т.о. m_x=np; D_x=npq

Пример 1.Реш-е: вероятнейшее число попаданий=МО. m_х=np=200·0,95=190; СКО: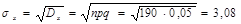

Для вычисления вер-ти появления события k раз в n испытаниях применяют формулу Бернулли. При больших n пользуются лок.теоремой Лапласа, к-рая пригодна при значениях вер-ти появления события в единичном испытании примерно удовлетворяет условию р≥1 при меньших значениях вер-ти и большом n выведем асимптотическую формулу Пуассона. Обозначим МО биномиальным распределение m_x=a=np=>р=a/n. Подставим р в формулу Бернулли и преобразуем:

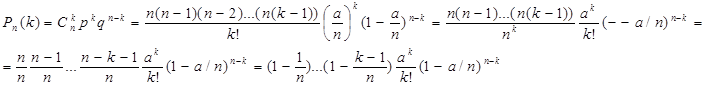
Учитывая, что n велико, найдем не саму величину P_n(k), а ее предельное значение при n→∞, к-рое дает приближенное значение P_n(k):

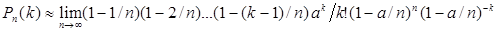
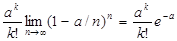
Т.о. для массовых, но редких событий (р мало) получаем формулу распределения Пуассона: P_n(k)≈(а^k/k!)e^-a.

Пример 2. n=5000; p=0.001;a=np=5.

Событие «потребитель получит не более 3 негодных деталей»=сумме несовместных событий «не повредится ни одной детали», «повредится одна», «-//- 2», «-//- 3». По т.сложения имеем, что: р(k≤3)=р(0)+р(1)+р(3)=е^-5+5е^-5+25/2 е^-5+125/6 е^-5=0,265