Из опр-я СВ нельзя заранее уверенно предсказать, какое возможное значение примет отдельная СВ в результате испытания (наблюдения), но если наблюдать достаточно большое число СВ, то для их суммы при выполнении некоторых условий утрачивается случ.характер и ее закономерности становятся почти достоверными. Это позволяет предвидеть ход явлений, обусловленных большим числом случ.причин. Теоремы, формулирующие условия, при к-рых это возможно, носят общее название з-на больших чисел.
Т.Чебышева: Если Х1, Х2,…,Хn попарно независимые СВ с равномерно ограниченными дисперсиями (например, не превышающими постоянного числа), то как бы ни было мало ε.>0 вер-ть неравенства |х‾-М‾(х)|< ε сколь угодно близко к1, если число СВ достаточно велико, где х‾иМ‾(х) обозн-ют ср.знач. СВ и их МО
х‾=1/nΣxi; M‾(x)=1/nΣМ(хi)
Др.словами, при выполнении условий т.Чебышева имеем: 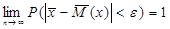 ,т.е. согласно т.Чебышева, если число независимых СВ достаточно велико, то почти достоверно, что отклонение средней величины СВ от средних знач.их МО будет (по абс.величине) сколь угодно малым.
,т.е. согласно т.Чебышева, если число независимых СВ достаточно велико, то почти достоверно, что отклонение средней величины СВ от средних знач.их МО будет (по абс.величине) сколь угодно малым.
Если СВ имеют одинаковые МО, к-рые обозначим а, то среднее значение МО всех СВ =а, в данном случае получим важный для практики случай 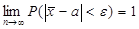 ,т.е.что х‾≈а. Другими словами, при выполнении условий т.Чебышева, ср.знач. с ожидаемым МО сколь угодно мало отличается от МО, что имеет большое практич.знач. Пусть производятся измерения некоторой физ.величины. Результаты такого измерения рассматриваются как СВ х1, х2,…хn результаты такого измерения рассматриваются как СВ х1, х2,…хn, к-рые могут принимать значения, далекие истинного значения измеряемой величины, т.е. от МО, но ср.знач. всех результатов измерения будет сколь угодно мало отличаться от истинной величины, если число измерений дост.велико.
,т.е.что х‾≈а. Другими словами, при выполнении условий т.Чебышева, ср.знач. с ожидаемым МО сколь угодно мало отличается от МО, что имеет большое практич.знач. Пусть производятся измерения некоторой физ.величины. Результаты такого измерения рассматриваются как СВ х1, х2,…хn результаты такого измерения рассматриваются как СВ х1, х2,…хn, к-рые могут принимать значения, далекие истинного значения измеряемой величины, т.е. от МО, но ср.знач. всех результатов измерения будет сколь угодно мало отличаться от истинной величины, если число измерений дост.велико.
Отметим, что ↑точности путём ↑числа измерений нельзя достичь сверх некоторого предела, т.к. этому препятствует ограниченная точность приборов, применяемых при измерениях. Если прибор вносит ошибку ±α, то результаты измерений будут получены с этой же ошибкой и их ср.знач. так же будут вычислены с этой ошибкой.
Т. Бернулли
Пусть производится n независимых испытаний по схеме Бернулли. Подсчитав число появления события (m «успехов») и поделив его на число испытаний n, получим относительную частоту «успехов».
W=m/n, к-рые принимают значения, близкие к вер-ти успехов в единичном испытании. Это доказал Бернулли в своей теореме, к-рая положила начало теории вер-тей как науки.
Т.Бернулли: Если в каждом из n независимых испытаний вер-ть р появления события А постоянна, то, как бы не было мало число ε>0, вер-ть нер-ва |m/n -p|< ε сколь угодно близка к 1, т.е.: 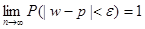
 2015-01-13
2015-01-13 533
533








