Числовые хар-ки ср.значения нескольких взаимно независимых одинаково распределенных СВ

Пусть имеем n взаимно незав. СВ: Х₁, Х₂,…, Х_n с одинаковыми з-ми распределения, а значит, с равными МО, дисперсиями и СКО: m_x1=m_x2=…=m_xn=a

D(X₁)=D(X₂)=…=D(X_n)=D; σ(Х₁)=σ(Х₂)=…=σ(Х_n)=σ

Найдем след.числовые хар-ки ср.значен.этих СВ: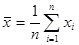

1)МО СВ Х‾: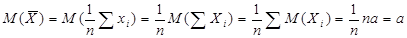

МО ср.знач.нес-ких СВ=МО каждой из них

2)дисперсия: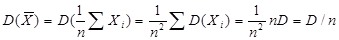

Дисперсия ср.арифметического n взаимно незав. СВ в n раз меньше дисперсии кадой из них.

3)СКО: 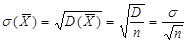. СКО ср.знач. n взаимно незав. СВ в √n раз меньше СКО каждой из них

Полученные результаты имеют практич.значение. Отдельные измерения нек-рой величины смогут значит. отличаться друг от друга (вследствие случ.ошибок), т.е. дисперсия (СКО) отдельных измерений м.б.дост. велика, а ср.знач. отдельных измерений дает результат тот более надежный для измеряемой величины, чем каждое из отдельных измерений, т.к. его дисперсия в n раз меньше