Изучение закономерностей массовых случайных явлений на практике осуществл.путём анализа результатов наблюдения статистических данных методами теор.вер.
Задачами мат.стат-ка явл.разработка методов получения стат.данных в результате наблюдений или эксперимента и их обработке, анализа полученных данных для практических целей.
Современную мат.стат.назв.наукой о принятии решений в усл.неопределенности.
Опр1: выб.совокупностью или выборкой называют сов-ть случайно отобранных объетов.
Опр2: генеральной сов-тью назыв совокупность объектов, из которых производится выборка.
Опр3: Объёмом совокупности (выборочной или генеральной назыв.число объектов этой совокупности).
Чтобы по данным выборки с достаточной уверенностью судить об интересующем как кол-вом признаке генер.сов-ти, т.е выборка должна быть репрезентативной. Для этого разработаны спец.способы отбора, кот.существенно зависят от особенностей изучаемых объектов.
В разл.областях техники эти способы отбора оговорены специальными руководящими документами, нормировками.
Осн.усл.репрезентативности выборки явл.случайность отбора, при кот.каждый объект должен искать одинаковую вероятность попасть в выборку.
Пусть при изучении объектов выборки наблюдались значения количественного признака х:
x1-n1-раз
x2-n2-раз
...
xn-nk-раз
n=Σ ni – объём выборки
Набл.значения xi назыв.вариантами
Последовательность вариант в возрастающем порядке назыв.вариационным рядом. Числа наблюдений ni разл.значений количеств.признака назыв.частотами, а их отношение к объёму выборки: wi=ni/n –относит.частоты.
Пример 1.Реш-е: w1=1/10; w2=0.3; w3=0.6
| хi | |||
| wi | 0,1 | 0,3 | 0,6 |
Опр4: Статистическим распределением назыв.перечень вариант и соотв.им частот или относит.частот.
При непрерывном распределении кол-венного признака статист.распределение задаётся последовательностью интервалов и соотв.им частот.
Пусть имеется стат.распредел.количеств.признака Х и х – число наблюдений при кот.наблюд.значение признака Х меньше х, n – общее число наблюдений.
Опр5: Эмпирической ф-цией распредел.назыв.ф-ция равная относит.частоте события Х<х: F*(x)=nx/n
Т.к по теореме Бернулли относит.частота приближенно равна вероятности события, то эмпирическая ф-ция распредел.явл. примерным представлением теорет.ф-ции распределения генеральной совокупности.
Св-ва эмпирической ф-ции распредел.такие же как и у теорет.ф-ции распределения, а именно:
1) значение эмпирической ф-ции принадлежит [0;1]
2) F*(x) –неую.ф-ция
3) Если xi наим варианта, а хk – наиб варианта, то F*(x)=0 при х≤xi и F*(x)=1 ghb x> xk
Пример 2. Реш-е: 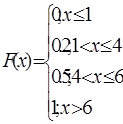
Опр6: Полигоном частот назыв.ломаная линия отрезка кот.соедин.точки (xi;ni)
По оси абцисс отклад.варианты xi, а по оси ординат- соотв.им частоты. Затем соедин.точки отрезками прямых и получают полигон частот.
Опр7: Полигоном относит.частот назыв.ломаную, соедин.точки, по оси ординат откладывают относит.частоты.
При неравномерном распределении признака стоят гистограмму, для этого интервал в кот.заключены все необходимые значения признака разбивают на несколько частичных интервалов длиной h и вычисляют для каждого частичного интервала сумму частот вариант попавших в i-ый интервал.
Опр8: Гистограммой частот назыв.ступенчатую фигуру сост.из прямоугольников, основаниями которых явл.частичные интервалы длиной h, а высоты равны отношениям ni/h
Опр9: Гистограммой относ.частот назыв.ступенчатая фигура, сост.из прямоугольников, основаниями которых явл.частичные интервалы длиной h, а высоты равны отношениям ni/h
Гистограмма относ.частот явл.статистическим аналогом графика плотностей вероятностей теорет.распределения.
Опр10: Модой M0 стат.распредел.назыв.варианта с наиб.частотой.
Опр11: Медианой Mе назыв.варианта для кот.значение эмпирической ф-ции распредел.ф-ции равно 0,5 f*(xe)=0,5. xe = Mе
Опр12: Размахом варьирования R назыв.разность м/д наиб.и наим.вариантами. R= xmax-xmin.
27. Статистические оценки параметров распределения. Выборочная средняя как оценка математического ожидания теоретического распределения. Генеральная и выборочная дисперсия. Исправленная дисперсия.
Статистические оценки параметров распределения
Пусть по результатам измерений нужно найти число, близкое к неизвестному значению измеряемого параметра θ теорет.распредел., это число θ* будем называть оценкой неизвестного параметра θ.
Т.О θ=θ*. Пусть в распоряжении исследователя имеются результаты измерений количественного признака х1, х2, …, хn т.е значение выборки объёма n. Если повторить измерение, то получатся другие n чисел, отличные от первых в силу влияния случ.причин. Результаты выборки поэтому можно рассчитывать как наблюдение над случайными величинами х1, х2, …, хn
Найти оценку параметра распределения – значит найти величину от результатов наблюдения: θ*= θ*(х1, х2, …, хn)
Опр1: стат.оценкой θ неизв.оценкой θ теор.распредел.назыв.ф-цию f(х1, х2, …, хn) от набл.случ.величины х1, х2, …, хn
Опр2: точечной назыв.стат.оценку, кот.определ.одним числом θ*=f(х1, х2, …, хn), где х1, х2, …, хn – результаты n наблюдений над количественным признаком X – выборка
Производя повторные выборки можно получить оценки принципиально отличающегося др.от друга θ1*, θ2*,…, θn*.
Т.О оценку θ* можно так же рассматривать как СВ, принимающую разл.значения. В связи с этим к оценке предъявл.требования несмещённости и состоятельности.
Опр3: несмещённой назыв.оценка θ* МО которой равно оцениваемому параметру, при любом объёме выборки: М(θ*)= θ.
Опр4: смещённой назыв.точечную оценку МО которой не равно оцениваемому параметру.
Несмещённость означает, что для оценки не имеет системат.ошибки.
Опр5: состоятельной назыв.оценке, которой n→∞ по вероятности стремится к оцениваемому параметру, т.е при сколь угодно малом ε>0 lim(n→∞) P(|θ-θ*|< ε)=1
Св-ва состоятельности обеспечивает уменьшение дисперсии при увеличении числа измерений и сближение оценки с измеряемым параметром при выполнении требования несмещённости.
Выборочная средняя как оценка математического ожидания теоретического распределения
Опр1: выборочной средней назыв.среднее арифмет.значение количественного признака выборочной совокупности
Если все значения признака х1, х2, …, хn то выборочная средняя наход.: х’= (х1, х2, …, хn)/n Если значение признака х1, х2, …, хn то выборочная средняя находится: х’= (n1х1, n1х2, …, nkхn)/n
Т.к х1, х2, …, хn – есть набл.значения СВ Х1, Х2,..,Хn c одинаковым МО Мxi =а и дисперсией Dxi=σ2,то МО и дисперсия среднего значения будут равны М(Х’)=a и D(X’)=σ2/n
Т.О среднее значение явл.несмещённой оценкой МО
Так же можно показать, что эта оценка состоятельна поэтому, если по нескольким выборкам достаточно большого объема из одной генеральной совокупности будут выбрана ср., то они будут мало отлич др.от друга в этом закл.св-во устойчивости выборочных средних.
Опр2: генеральной средней назыв.среднее арифмет.значение признака генеральной совокупности.
В следствии очень большого объёма генеральной совокупности генеральная средняя принимается равной МО теорет.распределения признака генеральной совокупности х’г=0
Вывод: несмещённый оценкой генеральной средней (МО) служит выборочное среднее х’B=1/n Σ nixi.
Пример 1. Реш-е: 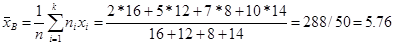
Замечание: Если первоначальные варианты xi – большие числа, то для упрощения расчёта нужно вычесть из каждой варианты одно и то же число С, т.е перейти к усл.вариантам Ui=xi-C
В качестве С нужно принять число, близкое к выборочной средней, а т.к выбор.средняя неизвестна, то число С выбирают «на глаз», тогда: х’B=С+1/n Σ niUi.
Пример 2. Реш-е: 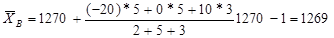
Генеральная и выборочная дисперсия. Исправленная дисперсия
Опр1: Генеральной дисперсией назыв.средн.арифмет.квадратов отклонений значений признака генеральной совокупности.
Генеральная среднеквадрат.отклонение- это квадратный корень из генеральной дисперсии, т.к средн.значение при большом объёме явл.оценкой МО – СВ, то генеральная дисперсия явл.оценкой дисперсии теорет.распредел.
Опр2: выбор.дисперсией назыв среднее арифметическое квадратов отклонений значений признаков выборки от выборочной средней.
Т.О дисперсия равна среднему из квадрату значения признакаминус квадрат средней. DB=x2’-(x’)2
Выбор.дисперсия явл.смещённой оценкой дисперсии теорет.распредел. (генеральной совокупности). Можно показать, что МО M(DB)=(n-1)/n*D
Для оценки генеральной дисперсии вводят исправл.дисперсию S2=(n-1)/n*DB
Испр.дисперсия явл.несмещённой оценкой генер.дисперсии: М(S2)=D
Замечание1: Если первоначальные варианты xi – большие числа, то нужно вычесть из всех вариант одно и тоже число С равное выборочной средней или близкое к ней, т.е перейти к усл.варианта Ui=xi-C.
Замечание2: Если первоначальные варианты явл.десятичными дробями с k десятичными знаками после запятой то, чтобы узбежать действий с дробями умножают первонал.варианты на пост.число, т.е переходят к усл.вариантам.
Пример 3. Реш-е:
| xi | |||||
| ni |
А) Х‾В=(92+94+103+105+106)/5=100
Б) 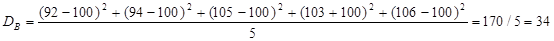
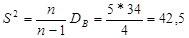
 2015-01-13
2015-01-13 2332
2332
