Математическое ожидание, дисперсия и СКО непрерывных СВ

Пусть все возможные значения НСВ ХÎ[a,b], разобьем отрезок на n частных отрезков внутри длиной ∆x_i. Выберем произвольно внутри каждого частного отрезка точку X_iBH и будем приближенно считать, что все возможные значения СВ Х из данного частичного отрезка сосредоточены в точке X_iBH, а вероятность того значения равна вероятности попадание СВ Х в этот частный отрезок длиной ∆x_i: P_i=P(x_i-1≤x≤x_i)=F(x_i)-F(x_i-1)=(dF(x))_i=F’(X_iBH)∆x_i=f(X_iBH)∆x_i

Взяв сумму произведений P_i X_iBH по всем частичным интервалам получим приближенно МО СВ Х, кот.мы представляли как ДСВ: М(Х)= Σ X_iBH f(X_iBH)∆x_i

Переходя к пределу при n→∞ и X_{i max}→∞ получим определ.интеграл:

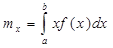(1)

Если возможные значения НСВ Х принадлежат всей оси ОХ, то интервал (1) становится несобственным: 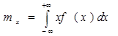(2), при этом требуется абсолютная сходимость интеграла(2)

Дисперсией НСВ аналогично с ДСВ назыв. МО квадрата отклонения СВ Х от её МО

Если НВС ХÎ(a,b), то дисперсия 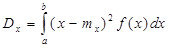(3). Формула (3) не очень удобна для вычислений, поэтому получим др.формулу. И имеем, что: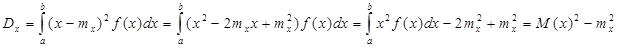

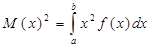
Т.О получена след.формула для вычисл.дисперсии:

D_x=M(X)²-m²_x

Аналогично с ДСВ для НСВ определ.СКО: значению σ_х =√D_x

Все св-ва МО и дисперсии рассмотренные для ДСВ справедливы и для НСВ.

23. Равномерное распределение. Распределение 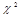. Распределение Стьюдента.

Равномерное распределение НСВ.

Опр: равномерным назыв.распределение НСВ, плотность распределения вероятностей которой постоянна в интервале, кот.принадлежат все возможные значения СВ.

Пусть НСВ ХÎ(a,b), тогда по св-ву 3) плотности распределения имеем, что: 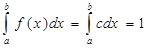|=> с(b-a)=1, где a<b |=> Плотность равномерного распредел.имеет вид: f(x) = система [0, если a≤x; 1/(b-a), если a<x≤b; 0,если x>b]

Найдём числовые хар-ки равномерного распределения:

1) МО: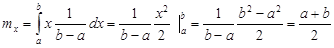

2)дисперсия: 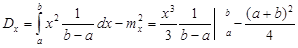=(b³-a³)/3(b-a) – (a²+2ab+b²)/4= (a²+ab+b2)/3 - (a²+2ab+b²)/4=(a²-2ab+b²)/12= (a-b)²/12

3)СКО: σ_х =√D_x=(b-a)/2√3=0,29

Равномерное распределение на практике встречается например, при округлении показателей измерит.прибора до ближайшего целого значения шкалы. Ошибка округления равна ±0,5 цены деления распределена по равномерному закону.

Распределение «хи квадрат»

Пусть Xi(i = 1, 2,..., n) — нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение-единице. Тогда сумма квадратов этих величинраспределена по закону 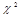(«хи квадрат») с k = n степенями свободы; если же эти величины связаны одним линейным соотношением, например

Σ X_i =nX’, то число степеней свободы k=n-1/

распределение «хи квадрат» определяется одним параметром—числом степеней свободы k.

С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Распределение Стьюдента

Пусть Z—нормальная случайная величина, причем M(Z) = Q, σ(Z) = l, а V — независимая от Z величина, которая распределена по закону 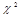с k степенями свободы. Тогда величина T=Z/(√V/k|), имеет распределение, которое называют t-распределением или распределением Стьюдента, с k степенями свободы.

Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы.

С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.