Б. НСВ
Пусть X - НСВ, которая в результате n испытаний приняла значения х1, х2,..., хn. Допустим, что вид плотности распределения f(х) задан, но не известен параметр Θ, которым определяется эта функция.
Функцией правдоподобия НСВ X называют функцию аргумента Θ:
L (х1, х2,..., хn; Θ) = f(х1; Θ) f(х2; Θ)... f(х„; Θ).
Оценку наибольшего правдоподобия неизвестного параметра распределения НСВ ищут так же, как в случае ДСВ.
Если плотность распределения f(х) НСВ X определяется двумя неизвестными параметрами Θ1 и Θ2, то функция правдоподобия является функцией двух независимых аргументов Θ1 и Θ2:
L = f(х1, Θ1, Θ2) f(х2, Θ1, Θ2,)... f(хn, Θ1, Θ2).
Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему:
Система [ ∂lnL/∂ Θ1=0 и ∂lnL/∂ Θ2=0]
Пример. Реш-е: составим ф-ци правдоподобия: L=p(x1,θ)*…*p(xn,θ)
Учитывая, что θ=pu; 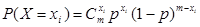 получим, что
получим, что 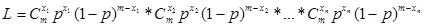
Напишем логарифмическую ф-цию правдоподобия: 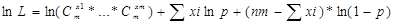
Найдем первую производную по р 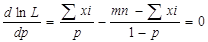 =>
=> 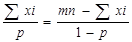
(1-р)Σхi=(nm-Σxi)p
Σхi=nmp; р= Σхi/nm
Найдем вторую произвожную по р 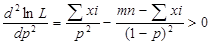 => р= Σхi/nm – точка max=> ее надо принять в кач-ве оценки наиб.правдоподобия неизв.вер-ть р биномиального распределения.
=> р= Σхi/nm – точка max=> ее надо принять в кач-ве оценки наиб.правдоподобия неизв.вер-ть р биномиального распределения.
р*= Σхi/nm. Очевидно, что если xi- появление события наблюдалось в ni опытах, то р*= Σхi*ni/nm
30. Точность оценки, доверительная вероятность и доверительный интервал. Доверительный интервал для оценки математического ожидания нормального распределения при известном и неизвестном СКО.
Точность оценки, доверительная вероятность (надежность). Доверительный интервал
Допустим получена оценка θ* неизвестного параметра θ, возникает вопрос с какой абсолютной ошибкой получена эта оценка.
Очевидно, что оценка θ* тем точнее определяет неизвестный параметр θ, чем меньше ε>0 в неравенстве |θ- θ*|<ε (1)
Т.О. точностью оценки называют число ε>0 оценивающие сверху абсолютную величину разности не известного параметра и его оценки.
Т.К. θ* является СВ и статистические методы не позволяют утверждать, что неравенство (1) осуществляется всегда, то можно говорить только о вероятности его выполнения.
Опр.: надёжность (доверительную вероятность) оценки θ и θ* назыв.вер-ть γ с которой выполнятеся неравенство (1)
Обычно надёжность оценки задаётся заранее, величиной близкой к единице, например 0,9; 0.95; 0,99; 0,999 и т.д.
Пусть вероятность того, что выполнится неравенство (1) равно γ: Р(|θ- θ*|< ε)= γ
Тогда из того, что |θ-θ*|<ε ó -ε<|θ- θ*|< ε ó θ*-ε<|θ|<θ*+ε, получим равенство:
Р(θ*-ε<|θ|<θ*+ε)= γ, кот.следует понимать так: вер-ть того, что неизвестный параметр заключается в интервале: (θ*-ε;θ*+ε), т.е θ=θ*±ε= γ этот интервал назв.доверительным интервалом.
Доверительный интервал для оценки математического ожидания нормального распределения при известном СКО.
Пусть количественный признак X генеральной совокупности распределен нормально с известным СКО.
Нужно найти доверительный интервал, покрывающие с надёжностью γ МО а этого распределения при известной выборочной средней х’.
Выборочную среднюю х’ рассматриваем как СВ (х’ меняется от выборки к выборке), а выборочные значения х1, х2, …, хn явл.одинаково распространенными (по нормальному закону) СВ с параметрами а и σ, выборочная средняя х’ так же распределена нормально с параметрами а и σ/(n)1/2, тогда имеем, что вероятность того, что Р(|х’-a|<ε)=2Ф(ε/(σ/(n)1/2)), вероятность равна заданной надёжностью, т.е Р(|х’-a|< ε)= γ
Обозначим ε/(σ/(n)1/2)=tγ, тогда 2Ф(tγ)=γ |=> Ф(tγ)=γ/2.
Значение tγ находят по известному значению γ/2 по таблице ф-ции Лапласа.
По найденному значению tγ из (1) определяют точность оценки: ε= (tγσ)/(n)1/2 и доверительный интервал для МО х’-ε<a< х’+ε с надёхностью γ.
Пример 1. Реш-е: Оценкой генер.СКО σ служит исправленная СКО σ=S=√[n/(n-1)] σВ= 3,21
Ф(tγ)= γ/2= 0,495. По таблице находим, что tγ=2,573
ε= (tγσ)/√(n)=0,653 |=> доверит.интервал: 11,62-0,65<a<11,62+0,65; 10,97<а<12,27
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном СКО.
При неизвестном СКО генеральной совокупности нельзя воспользоваться ф-цией Лапласа, в этом случае для нахождения доверительного интервала по данным выборки строится СВ(с возможными значениями t): T= (х’-a)/(σ/(n)1/2), которое имеет распределение, называемое распределением Стьюдента.
Доказано, что плотность вероятности распределения Стьюдента S(t;n) не зависит от неизвестных параметров a и S, а определяется только объёмом выборки n.
Плотность распределения Стьюдента – чётная относительно t, поэтому имеем, что: Р(|((х’-a)(n)1/2)/s)|<tγ= 2∫S(t;n)dt=γ
Для определения tγ по заданной надёжности γ и объёму выборки n составлена таблица t(γ;n).
При увеличении объёма выборки распределения Стьюдента быстро приближается к нормальному (с нормальными параметрами а=0 и σ=1), поэтому при n≥30 можно пользоваться ф-цией Лапласа |=> Решение поставленной задачи выполняется след.образом: по заданной надёжности γ и объёму выборки n по таблице ф-ции t(γ;n) наход.значения tγ. Далее находится точность оценки по формуле аналогичной формуле ε= (tγσ)/(n)1/2 , где S=[n/(n-1)]1/2 σB
Доверительный интервал для оценки МО с заданной надёжностью определяется неравенством х’-ε<a< х’+ε.
Пример 2. Реш-е: Результат измерения зависит от очень большого числа случайных причин, действующих независимо др.от друга. Поэтому считаем его распределение по закону близкого к нормальному. При γ=0,99 и n=9 по табл. t(γ;n)=3,36, вычислим S=√[n/(n-1)] σВ=4,56; ε= (tγσ)/√(n)=5,11
Доверит.интервал для истинного значения измеряемой величины имеет вид: 32,86-5,11<a<32,86+5,11; 27,75<a<37,97
 2015-01-13
2015-01-13 626
626








