Методы расчета характеристик выборки

Покажем на примере метод непосредственной обработки выборки.

Пример: Некоторая физ.величина z измерена 9 раз. Найти вероятнейшее значение этой величины, среднеквадрат.ошибки единичного результата измерения и вероятнейшего значения, предельную ошибку единичного измерения и установить имеются ли среди измеренных величин промахи.

С надёжностью 0,99 найти доверит.интервал для оценки истинного значения измеренной величины. Результаты измерений связаны в табл.в порядке возрастания.

Пример. Решение: Вероятнейшее значение измеренной величины, это её среднее значение

Ž= Σz_i/n = 146,8/9=16,31

Найдём среднее из квадратов значение: Ž²= Σz_i²/n=2309,92/9=266, 658

Вычислим исправленную среднеквадратическую ошибку единичного измерения: S_z=корень из [n/(n-1) (Ž^2- (Ž)²)]=0,8498

Среднеквадратическая ошибка выроятнейшего (среднего) значения равна: S_Ž= S_z/(n)^1/2 = 0,2833

Предельная ошибка единичного измерения принимается в три раза большей среднеквадрат.ошибки единичного измерения:

ε_пред=3S= 2,5494

Возможные измеренные значения должны находиться в пределах: Ž-ε_пред<z_i<Ž+ε_пред

16,31-2,55<z_i<16,31+2,55

13,76<z_i<18,86

Приведенные результаты не входят за эти пределы, промахов нет. Если бы промахи были, то их нужно было бы отбросить и произвести обработку выборки снова.

По таблице значений t(γ;n) составленной для распределения Стьюдента γ=0,99 и n=9, t(γ;n)=3,36

Точность оценки ε= t_γ S_Ž = 3,36*0,2833=0,952

Доверительный интервал для оценки истинного значения измеренной величины имеет вид: Ž-ε<z_чист< Ž+ε

16,31-0,95< z_чист <16,31+0,95

15,36< z_чист <17<26

32. Обработка результатов наблюдений. Метод наименьших квадратов. Линейная аппроксимация экспериментальных данных. Коэффициент корреляции и его свойства.

Обработка результатов наблюдений. Метод наименьших квадратов.

Неизвестные функциональные независимости на практике устанавливаются по средствам измерений.

Пусть например, исследуются функциональная зависимость y=f(x), где ф-ция f(x) неизвестна.

При различных значениях х₁, х₂, …, х_n известных точно измерены с ошибками значения соответствующих им у₁, у₂,…,у_n; y_i=f(x_i); x_i=1,…,n

При полном отсутствии информации о характере ф-ции f(x) нельзя получить достаточно удовлетворенное её приближение. В этом случае, построив в декартовых координатах пары (x_i;y_i) и соединив их ломаной линией получим график мало напоминающий график ф-ции y=f(x)

По расположению экспериментальных точек и виду ломаной линии предполагая св-ва гладкости ф-ции y=f(x), а так же основываясь на некоторых предположениях, вытекающих из сути изучаемого явл.можно выдвинуть гипотезу о виде предполагаемой зависимости.

Гипотетическая ф-ция должна зависеть кроме аргумента от нескольких параметров a,b,c.. кот.нужно подобрать так, чтобы полученная ф-ция своими значениями в точках х₁, _х2, …, х_n была возможно ближе к измеренным значениям у₁, у₂,…,у_n

Наилучшим приближениям будет такая ф-ция для кот.сумма квадратов отклонений, измеренных значений от вычисленных значений от вычисленных значений ф-ции (при соответствующих значениях аргумента) была линейной. В этом заключается метод наименьших квадратов.

Пусть например, гипотетическая ф-ция зависит от 2-х параметров f(x,a,b), тогда сумма отклонения имеет вид F(a,b)= Σ(f(x,a,b)- y_i)² (1)

Сумма (1) надо минимизировать. Известно, что ф-ция нескольких переменных достигает экстремума в точках, где частные производные равны нулю, т.о. система [F’_a(a,b)=0 и F’_b(a,b)=0] (2)

Решая полученную систему найдём параметры a и b, дающие наилучшие приближения ф-ции к экспериментальным данным.

Линейная аппроксимация экспериментальных данных. Коэффициент корреляции и его свойства.

Пусть экспериментальные данные позволяют предполагать линейную зависимость между количественными признаками Х и У: y=kx=b

Согласно формулам (1) и (2) имеем, что F(k,f)= Σ(kx_i+b-y_i)²

Система [F’_k(k,b)= Σ2x_i(kx_i+b-y_i)=0 и F’_b(k,b)= Σ2(kx_i+b-y_i)=0]

Система [k= Σx_i²+b Σx_i= Σx_iy_i и k= Σx_i+bn= Σy_i] (3)

Разделив для удобства обе части полученных ур-ний на n будем иметь: kх’²+bх’= х’ý и kх’+b=ý, где чертов обозначены средние значения.

х’ý=1/n Σx_iy_i

Решим полученную систему с помощью формул Крамера: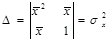

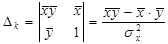
K=Δk/Δ= (х’ý- х’*ý)/σ_x² (4)

Используем второе Ур-ние системы (3) b= ý-kх’

Подставляя значение в Ур-ние прямой будем иметь: y=kx+b и y=kx+ý- kх’ |=> y-ý=k(x- х’) (5)

Т.О прямая проходит через точку (х’;ý), координаты кот.явл.средними значениями признаков.

Преобразуем формулу(4): k=(х’ý- х’*ý)/σ_xσ_y ^*(σ_x/σ_y)=r_B σ_x/σ_y

Т.О вводится величина r_B==(х’ý- х’*ý)/σ_xσ_y (6), уот.назыв.выборочным коэ-том корреляции и имеет самост.значение, тогда k= r_B σ_x/σ_y (7)

Учитывая (5) и (7) можно получить ур-ние прямой в след.виде: (y-ý)/ σ_y=(x-х’)/ σ_x (8)

Найдем минимум среднего значения квадратов отклонения эксперимент.точек от теоретических при найденных значениях k и b: 1/n F(k;b=1/n Σ(kx_i+b-y_i)² = 1/n Σ(kx_i+y-kх’-y_i)² = 1/n Σ(k(x_i-х’)-(y_i -ý))² =k/n Σ(x_i-х’)²+² 1/nΣ (y_i -ý))²-2k/n Σ(x_i-х’)(y_i -ý)= k²σ_x²+σ_y²-2n/k Σ(x_iy_i -x_iý- х’y_i-х’ý)= k²σ_x²+σ_y²-2k (1/n Σx_iy_i-ý Σx_i/n- х’ Σy_i/n+ х’ý)= k²σ_x²+σ_y²-2k(х’ý-ýх’-х’ý+х’ý)= k²σ_x²+σ_y²-2k(х’ý-ýх’)=r²_B σ_y²/σ_x²* σ_x²-2r_B σ_y/σ_x r_B σ_yσ_x = σ_y²(1- r²_B)

Т.О F(k;b)_min=n σ_y²(1- r²_B) (9). Величина определяющая (9) назыв.остаточной дисперсией,т.к сумма квадратов отклонений неотрицательна, то (1- r²_B)≥0 |=> |r_B|≤1 (10).

Положим в (9) |r_B|=1, тогда F(k;b) _{min min}=0, т.е. минимум всех квадратов отклонений достигает своего наим.значения равного нулю, т.е все квадраты отклонений, а значит и сами отклонения равны нулю, др.словами излучаемая зависимость действительной линейной ф-ции и ошибки наблюдения отсутствуют.

Если r_B=0, то остаточная дисперсия имеет наиб.значение F(k;b) _{min max} =n σ_y²

Как следует из уравнения (8) у=ý, т.е значение величины У не зависят от значений Х.

Теорией вероятностей доказыв.,что чем ближе выборочный коэф-т корреляции по модулю к единице, тем теснее линейная связь м/д признакми Х и У и наоборот, чем меньше по модулю r_B, тем слабее линейная связь м/д признаками.

Отметим, что малая величина r_B (по модулю) свидетельствуют о слабости или отсутствии связи именно линейной, а не об отсутствии связей какого-либо другого вида служит другая величина – корреляционное отношение.

Пример. Реш-е: наносим эксперим.точки на чертеж ….

По расположению точек полагаем возможной лин.апроксимацию.

х‾=20/5=4; х‾²=90/5=18; у‾=14,5/5=2,9; у‾²=50,35/20=10,07; σ_х=√2;σ_у=√1,66; (ху)‾=50,5/5=10,1;

r_В=((ху)‾- х‾*у‾)/σ_хσ_у= -0,8232

|r_В|≈1, поэтому лин.св.м/у признаками можно считать дост.тесной. Ур-е прямой по формуле: (y-ý)/ σ_y=(x-х’)/ σ_x: у=-0,75х+5,9

Найдем знач-е апроксимир-ей ф-ции для 2 крайних точек:

У(2)=-0,75*2+5,9=4,4; у(6)=-0,75*6+5,9=1,4. По этом точкам строим прямую, по расположению к-рой относит.измерений точек визуально можно отметить относит.правильность расчета.