Тестовые задания. S: проекции вектора 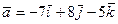есть

I:

S: Проекции вектора есть

-:

-:

-:

-:

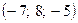
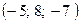
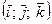
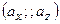
I:

S: Признак коллинеарности двух ненулевых векторов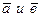

-:

-:

-:

-:

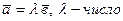
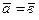
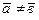
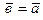
I:

S: Три ненулевых вектора 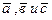компланарны если

-:

-:

-: -:

-:

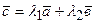
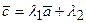
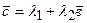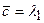
I:

S: Каждый вектор 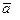равен

-: произведению его модуля на орт

-: единичному вектору

-: нулевому вектору

-: произведению его модуля на любое число

I:

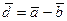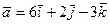S: Координаты вектора , где и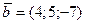

-: (2; -3; 4)

-: (-1; 2; 3)

-: (9; 2; 6)

-: (1; 5; 3)

I:

S: Проекции вектора 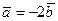,где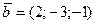

-: (-4; 6; 2)

-: (1; 5; 3)

-: (-6; 9; -3)

-: (-2; 2; 3)

I:

S: Вектор параллельный вектору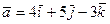

-:

-:

-:

-:

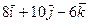
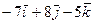
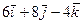
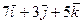
I:

S: Координаты орта 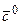вектора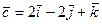

-:

-:

-:

-:

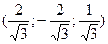
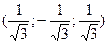
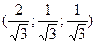
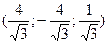
I:

S: Луч образует с двумя осями координат углы в 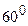, тогда угол наклона к третьей оси

-:

-:

-:

-:

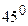
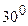
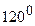
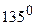
I:

S: Координаты вектора 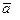, если 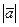=3 и углы между вектором и координатными осями равны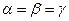

-:

-:

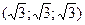
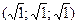
-: (3;3;3)

-: (0;0;0)

I:

S: Если один из трёх вектора 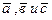нулевой, то данные векторы

-: компланарны

-: равны

-: совпадают

-: коллинеарны

I:

S: Если два из трёх вектора 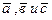коллинеарны, то данные векторы

-: компланарны

-: нулевые

-: равны

-: совпадают