2015-01-21
362
Скалярным произведением ненулевых векторов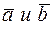 
называется число, равное произведению длин этих векторов на косинус угла 
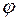между ними. Обозначение 
.
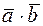Таким образом,
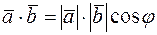(1)
 | |
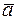
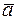
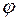
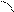
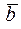
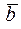
Формулу (1) можно записать в виде
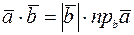или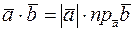 
.
Свойства скалярного произведения:
1. 
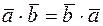
2. 
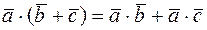
3. 
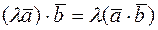
4. 
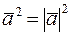
5. 
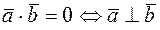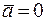(или 
,или 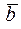=0). В частности: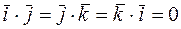 
Векторы 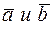, скалярное произведение которых равно нулю, называются ортогональными.
Если векторы заданы своими координатами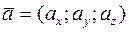 
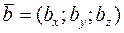, то
.
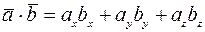Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
