2015-01-21
2905
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты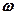 
. Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.
Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту (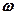 рез — частоту, при которой амплитуда А смещения (заряда) достигает максимума,— нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по 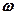и приравняв нулю, получим условие, определяющее 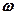рез:
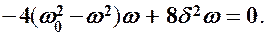
Это равенство выполняется при 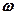= 0, ± 
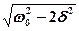, у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота
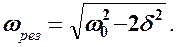(148.1)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте 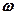рез называется резонансом (соответственно механическим или электрическим). При 
<< 
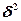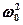значение 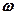рез практически совпадает с собственной частотой 
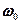колебательной системы. Подставляя (148.1) в формулу (147.8), получим
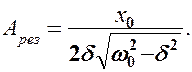(148.2)
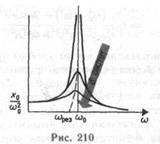
На рис. 210 приведена зависимость амплитуды вынужденных колебаний от частоты при различных значениях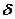 
. Из (148.1) и (148.2) вытекает, что чем меньше 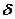, тем выше и правее лежит максимум данной кривой. Если 
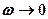, то все кривые (см. также (147.8)) приходят к одному и тому же, отличному от нуля, предельному значению 
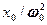, так называемому статическому отклонению. В случае механических колебаний = 
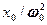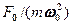, в случае электромагнитных — 
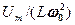. Если 
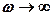,то все кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.
Из формулы (148.2) вытекает, что при малом затухании (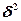 << 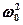) резонансная амплитуда смещения (заряда)
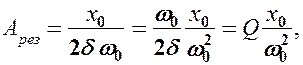
где Q — добротность колебательной системы (см. (146.8)), 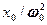— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше 
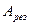. На рис. 211 представлены резонансные кривые для амплитуды скорости (тока), Амплитуда скорости (тока)
максимальна при 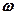рез = 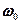и равна 
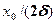, т. е. чем больше коэффициент затухания 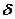, тем ниже максимум резонансной кривой.
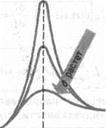
Рис. 211
Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна (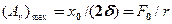
, а амплитуда тока при электрическом резонансе
Из выражения tg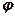 
= 2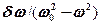 
(см. (147.9)) следует, что если затухание в системе отсутствует ( 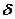= 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях 
.
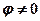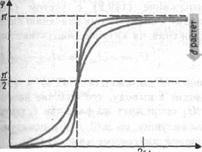
Рис. 212
Зависимость 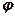от 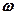при разных коэффициентах 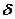графически представлена на рис. 212, из которого следует, что при изменении 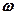изменяется и сдвиг фаз 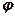. Из формулы (147.9) вытекает, что при 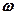= 0 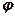= 0, а при 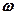= 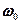независимо от значения коэффициента затухания 
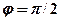, т. е. сила (напряжение) опережает по фазе колебания на 
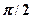. При дальнейшем увеличении 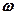сдвиг фаз возрастает и при >> 
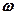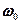
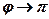, т.е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.
Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.
