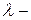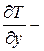При рассмотрении турбулентных потоков в реальных жидкостях и газах, наряду с переносом количества движения (импульса), часто приходится одновременно иметь дело учитывать с переносом тепла и вещества (тепломассобменом).
Практически интересные задачи тепломассопереноса в турбулентных потоках обычно допускают простую стратификацию по температуре и стратификацию по скорости, о которой мы говорили в предыдущих параграфах. Пользуясь идеей Буссинеска о предании формуле турбулентного трения того же вида, что и для ламинарного течения, а именно в виде закона Ньютона, можно и турбулентным потоком тепла и вещества придать вид, формально обобщающий известны уже нам законы Фурье и Фика.
Закон Фурье
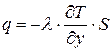
Где 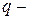 тепловой поток
тепловой поток
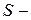 площадь теплообмена
площадь теплообмена
Первый закон Фика устанавливает для стационарной диффузии пропорциональность плотности потока 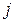 диффундирующих частиц градиенту их концентрации
диффундирующих частиц градиенту их концентрации 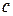 :
:
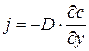
Где 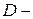 коэффициент диффузии;
коэффициент диффузии;
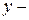 координата.
координата.
Второй закон Фика описывает нестандартный случай, он следует из первого закона Фика при учёте изменения концентрации диффундирующих частиц со временем 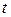 :
:
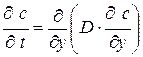
При 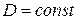 2-ой закон Фика представляет собой уравнение диффузии
2-ой закон Фика представляет собой уравнение диффузии
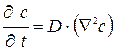
 Обозначим соответственно через
Обозначим соответственно через 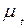 ,
, 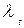 ,
, 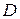 - коэффициенты турбулентного переноса импульса (количества движения, тепла и концентрации примеси). Тогда в принятой стратификации будем иметь следующие выражения для касательного напряжения трения
- коэффициенты турбулентного переноса импульса (количества движения, тепла и концентрации примеси). Тогда в принятой стратификации будем иметь следующие выражения для касательного напряжения трения 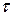 , потока тепла
, потока тепла 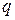 и потока вещества
и потока вещества 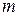 :
:
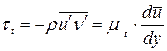 ;
;
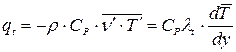 ;
;
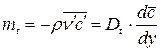 .
.
Как это непосредственно следует из правых частей выражений (10), (18) и аналогичного им уравнения турбулентной диффузии, полный перенос импульса, тепла и вещества может быть представлен как сумма соответствующих молекулярного (ламинарного) и молярного (турбулентного) переносов:
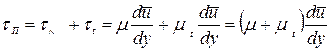 ;
;
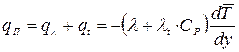 ;
;
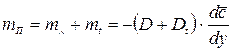 .
.
В основе общей теории турбулентного переноса лежит представление о том, что одни и те же объёмы жидкости или газа, участвуя в пульсационном движении, одновременно переносят количество движения, тепло и вещество.
При этом, казалось бы, что коэффициенты 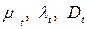 должны быть пропорциональны друг другу. И это действительно было так, если бы переносимая субстанция (количество движения, тепло, примеси вещества) не взаимодействовала с окружающей средой, вела себя пассивно в процессе переноса. Если представить себе, что на некотором пути смешения
должны быть пропорциональны друг другу. И это действительно было так, если бы переносимая субстанция (количество движения, тепло, примеси вещества) не взаимодействовала с окружающей средой, вела себя пассивно в процессе переноса. Если представить себе, что на некотором пути смешения  , как это требует теория Прандтля, количество движения сохраняется, то отсюда не следует, что на том же пути
, как это требует теория Прандтля, количество движения сохраняется, то отсюда не следует, что на том же пути 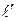 будет сохраняться и количество тепла и вещества.
будет сохраняться и количество тепла и вещества.
Простейшим и практически часто достаточным является допущение о пассивности переносимой субстанции 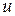 , следовательно, о равенстве турбулентных чисел Прандтля
, следовательно, о равенстве турбулентных чисел Прандтля
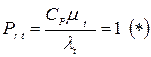 и Шмидта
и Шмидта 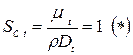
Они являются безразмерными критериями, характеризующими связь между процессами переноса импульса, тепла и вещества.
В этом случае задача определения параметров течения газа (жидкости) упрощается, т.к. достаточно определить один из турбулентных коэффициентов, чаще 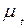 и остальные легко определяются из выражений
и остальные легко определяются из выражений 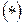 .
.
 2014-09-04
2014-09-04 956
956