2014-09-04
1674
Система уравнений Навье-Стокса для описания турбулентного движения вязкой несжимаемой жидкости при отсутствии массовых сил может быть представлена в векторно - тензорной форме:
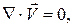(1.1)
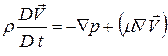. (1.2)
В скалярно-тензорной форме уравнения неразрывности и изменения количества движения записывается так:
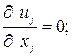(1.3)
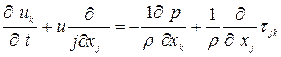. (1.4)
С учётом уравнения неразрывности (1.3) уравнение (1.4) может быть представлено в виде
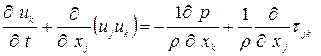. (1.4а)
В уравнениях (1.1)-(1.4) используемые индексы определяют направления декартовой системы координат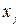 
(здесь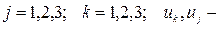 
декартовые составляющие скорости в направлении соответствующих осей; 
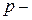давление; 
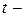время; 
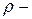плотность жидкости; 
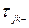составляющие тензора вязких напряжений;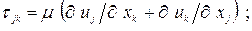 
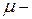коэффициент динамической (молекулярной) вязкости; 
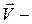вектор местной скорости потока;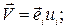 
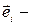единичные векторы; 
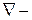оператор Гамильтона; 
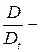полная производная повремени).
С учётом уравнения неразрывности член, определяющий касательное трение, записывается как
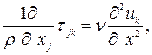(1.5)
где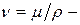 
коэффициент кинематической вязкости.
Как уже отмечалось, согласно подходу Рейнольдса, любые мгновенные значения гидродинамических параметров потока представляются в виде суммы осреднённой величины (во времени) и её пульсационной составляющей. Фактически это означает, что гидродинамическая величина является случайной, осреднение которой во времени даёт её математическое ожидание, а пульсационная составляющая которой – дисперсия случайной величины. Обозначая осреднённую во времени величину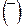 
, а пульсационную 
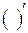, для составляющей скорости 
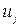, например, можно записать 
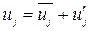. Тогда уравнение (1.3) примет вид
|
|
|
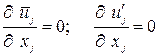(1.3а)
Для давления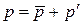 
, для трения 
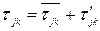. Естественно, что 
, 
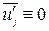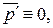
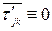. Следует отметить, что среднее значение 
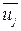, несмотря на интегрирование времени:
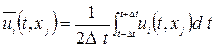
Может изменяться во времени. Это означает, что период интегрирования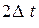 
должен быть малым по сравнению с характерным временем нестационарного изменения 
.
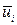Применяя операцию осреднения во времени к уравнению (1.4а), получим
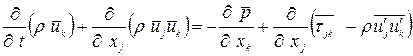, (1.6)
Где -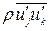 
- составляющие тензора напряжений Рейнольдса или рейнольдсовых напряжений. Они являются дополнительными (шестью) неизвестными к гидродинамическим параметрам осреднённого движения (
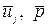). Таким образом, система уравнений (1.3а) и (1.6) является незамкнутой.
Вопросы замыкания полученной системы уравнений решаются на различном уровне сложности, и им будет посвящена значительная часть курса. Простейший путь – использование эмпирической информации о характеристиках турбулентности, наиболее сложный заключается в выводе уравнений относительно рейнольдсовых напряжений.
