Частным случаем (1.15) является уравнение для кинетической энергии турбулентных пульсаций 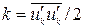 . Если в уравнении (1.15) принять
. Если в уравнении (1.15) принять 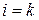 , просуммировать члены по всем
, просуммировать члены по всем 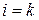 и умножить полученное уравнение на 1/2, то в результате получаем
и умножить полученное уравнение на 1/2, то в результате получаем
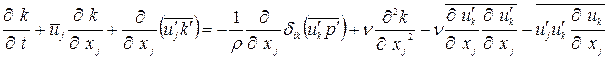
(1.16)
Или
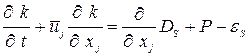 , (1.16а)
, (1.16а)
Где
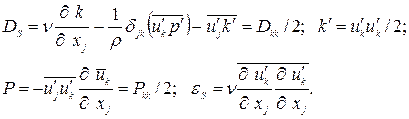
Уравнение (1.16) по виду не отличается от уравнения (1.15), за исключением того, что член перераспределения в нем отсутствует. Члены генерации 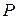 , диффузии
, диффузии  и диссипации
и диссипации 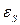 - такие же, как в уравнении (1.15). Отметим, что
- такие же, как в уравнении (1.15). Отметим, что 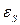 называют изотропной диссипацией турбулентности или псевдодиссипацией. Вместо
называют изотропной диссипацией турбулентности или псевдодиссипацией. Вместо 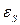 вводят в рассмотрение функцию, которую называют истинной диссипацией, или скоростью диссипации турбулентной энергии:
вводят в рассмотрение функцию, которую называют истинной диссипацией, или скоростью диссипации турбулентной энергии:
 (1.17)
(1.17)
Следует добавить, что  , если диссипирующие (мелкомасштабные) турбулентные вихри являются изотропными, т.е. статически не зависящими от направления потока. Во многих случаях равенство
, если диссипирующие (мелкомасштабные) турбулентные вихри являются изотропными, т.е. статически не зависящими от направления потока. Во многих случаях равенство 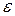 и
и 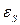 близко к действительности. Исключение составляют пристеночные течения, а именно слой, примыкающий к стенке(так называемый вязкий подслой). Также отметим, что формальный переход в уравнение (1.16) от
близко к действительности. Исключение составляют пристеночные течения, а именно слой, примыкающий к стенке(так называемый вязкий подслой). Также отметим, что формальный переход в уравнение (1.16) от 
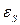 к
к 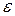 сказывается на изменении в нём диффузионного члена, который в этом случае принимает вид
сказывается на изменении в нём диффузионного члена, который в этом случае принимает вид
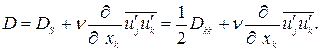
Независимо от формы записи уравнения (1.16) неизвестными в нём являются корреляции пульсаций давления и скорости; двойные 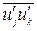 и тройные
и тройные 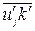 корреляции пульсаций скорости, а также диссипативный член
корреляции пульсаций скорости, а также диссипативный член 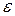 или
или 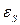 .
.
 2014-09-04
2014-09-04 1202
1202
