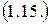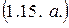2014-09-04
1065
Вывод уравнений для рейнольдсовых напряжений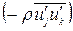 
начинается с преобразования уравнения (1.4а). Умножая его на 
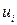, получим
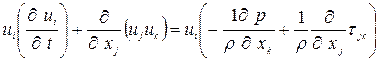. (1.7)
Поменяем индексы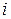 
и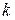 
местами:
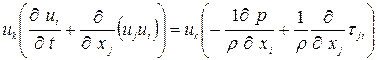. (1.8)
Суммируя (1.7) и (1.8) получим
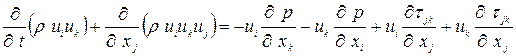(1.9)
В результате осреднения во времени уравнения (1.9) имеем
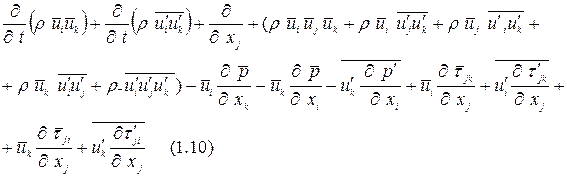
Умножим уравнение (1.6) на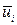 
:
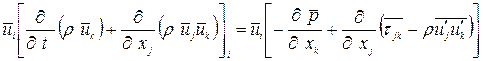. (1.11)
Меняя в последнем уравнении местами индексы 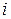и 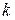, получаем
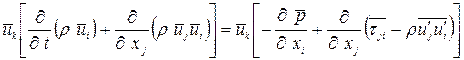. (1.12)
Сумма последних двух уравнений даёт уравнение вида
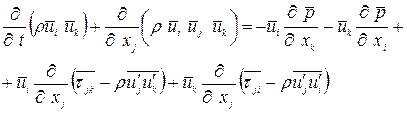
(1.13)
Уравнение переноса турбулентных или рейнольдсовых напряжений получается вычитанием из уравнения (1.10) уравнения (1.13):
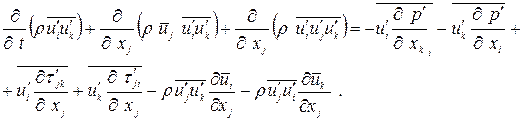(1.14)
Следует отметить, что первые четыре члена в правой части и член с тройной корреляцией в левой части уравнения (1.14) являются неизвестными.
Преобразуем(1.14). Запишем первые два члена в правой части как
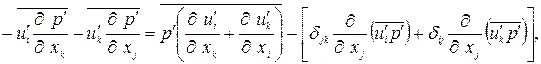
где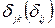 
- единичный тензор.
Третий и четвёртый члены в правой части преобразуются с учётом уравнения неразрывности следующим образом:
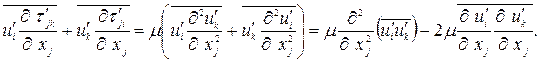
Таким образом, (1.14) записывается в виде
|
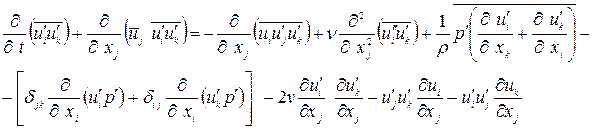
или
|
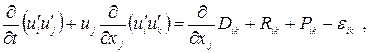
Где
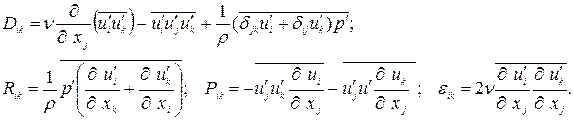
Левая часть уравнения построена по форме обычного уравнения переноса (равна субстанционной (полной) производной от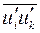 
). Для четырёх членов в правой части приняты следующие обозначения:
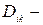диффузией член, обусловленный молекулярной диффузией, турбулентной диффузией перемешивания посредством взаимодействия пульсаций скорости и турбулентной диффузией давления посредством корреляций давления и скорости;
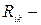член перераспределения, описывающий обмен энергией между отдельными составляющими 
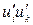вследствие корреляции давления и напряжения трения;
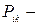член порождения или генерации турбулентности, определяющийся произведением рейнольдсовых напряжений и средних градиентов скорости (характеризует перенос энергии от осреднённого течения к пульсационному);
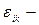диссипативный член, характеризующий преобразование энергии, подведённой к пульсационному течению, в частности, перенос энергии крупномасштабных вихрей к мелкомасштабным диссипирующим вихрям.
Полученное уравнение(1.15) не является замкнутым, так как неизвестны величины: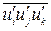 
, 
, 
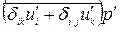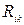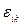. Для замыкания (1.15) требуется указанные члены соответствующим образом моделировать, используя эмпирические данные или иные соображения, подчас эвристического характера.
