2015-01-21
2162
Для стационарного процесса 
(
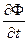=0) в диффузионном приближении для тепловых нейтронов (поток 
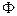в этом случае не зависит от энергии) уравнение (1.42) сильно упрощается:
 | (1.43) |
или
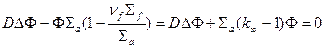 | (1.44) |
где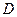 
- коэффициент диффузии:
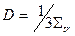 | (1.45) |
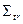- транспортное макроскопическое сечение, учитывающее анизотропию нейтрон-ядерного рассеяния,
,
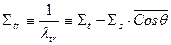Здесь величина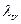 
называется транспортной длиной, 
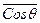- средний косинус угла рассеяния, 
)
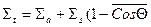Оператор Лапласса для одномерных геометрий записывается:
для сферической геометрии -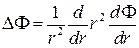 
,
для цилиндрической -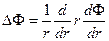 
,
для бесконечной плоскости -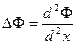 
Вводя обозначения
æ 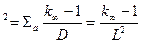 | (1.46) |
где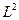 
- квадрат длины диффузии,
,
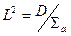получим уравнение:
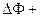æ2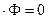 
Величина æ - называется материальным параметром реактора.
Краевые условия задачи: непрерывность Ф на участке от 0 до R и обращение Ф в нуль на экстраполированной границе реактора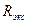 
(
):
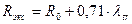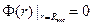
Известно, что среди множества решений волнового уравнения типа
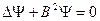 | (1.47) |
существует лишь единственное, удовлетворяющее краевым условиям и условию не отрицательности функции распределения потока нейтронов.
Для сферического реактора решение ищется в виде:
,
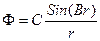где С – произвольная константа. Выражение (1.47) является решением стационарной задачи не для любых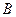 
, а только для
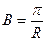 | (1.48) |
В данном случае величина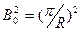 
является минимальным собственным значением оператора Лапласса для сферической геометрии.
Свои собственные значения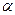 
существуют для реакторов любых форм и размеров и носят название геометрического параметра реактора.
Условием существования в ограниченной размножающей среде без внешнего источника стационарного состояния поля нейтронов является равенство материального и геометрического параметров:
| æ =Bo | (1.49) |
Условие (1.49) и размер реактора, соответствующий этому условию называется критическими.
Для сферического реактора из условия (1.48) легко найти критический радиус реактора
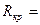 p/æ | (1.50) |
или, подставляя (2.22) в (2.25) получим
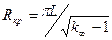
Объем размножающей среды, находящийся в стационарном состоянии, называется критическим, а масса делящегося вещества в этом объеме – критической.
Решение односкоростного диффузного уравнения для реактора, имеющего форму бесконечно протяженной пластины толщиной Н:
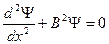
с краевыми условиями
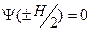
есть
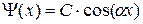
Геометрический параметр в этом случае:
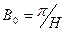
Из условия В 0 = æ находим критическую толщину плоского реактора
Н кр=p/æ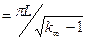 
Для цилиндрического реактора радиусом R решение соответствующего уравнения
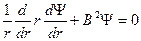
с краевыми условиями
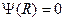
имеет вид:
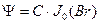
где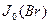 
- функция Бесселя нулевого порядка. Из краевого условия находим корень уравнения 
, 
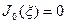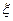= 2,405.
Геометрический параметр для цилиндрического реактора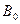 
.= 2,405/ R, а критический радиус
R = 2,405/ æ =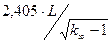 
Решения уравнения для цилиндрического реактора конечной высоты.
Решение уравнения для двухмерного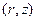 
цилиндра
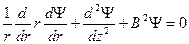
находят методом разделения переменных, полагая
,
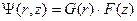где 
– решения задачи для бесконечного цилиндра,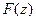 
– решение для бесконечной пластины.
Геометрический параметр для конечного цилиндра
,
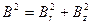где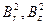 
, – геометрические параметры для бесконечного цилиндрического и бесконечного плоского реакторов, соответственно.
Решение уравнения:
,
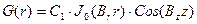где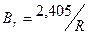 
; 
.
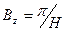Критическое условие имеет вид:
æ2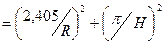 
.
Минимальное количество топлива определенной конфигурации и состава, в котором kэф=1 (r=0),называют критической массой, а соответствующие размеры размножающей среды – критическими размерами.
Минимальные критические размеры и массу имеет размножающая среда в форме шара. Для 235U такой шар без отражателя имеет массу ~ 48 кг и радиус ~ 8,5 см. Используя отражатель критическую массу можно уменьшить в 2–3 раза.
