| Определение | 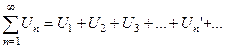 , , 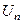 - действительные числа произвольного признака
В частности, - действительные числа произвольного признака
В частности, 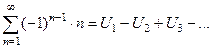 , , 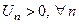 - знакочередующийся ряд - знакочередующийся ряд
| |||
| Абсолютная и условная сходимость знакопеременных рядов | 1. 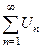 и и 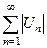 сходятся сходятся 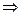 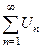 - абсолютно сходится
2. - абсолютно сходится
2. 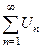 сходится, а сходится, а 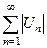 расходится расходится 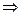 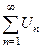 - условно сходится - условно сходится
| |||
| Достаточные признаки сходимости знакопеременных рядов | ||||
| Признак абсолютной сходимости | Признак Лейбница | |||
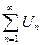 - знакопеременный - знакопеременный
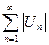 сходится сходится 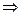 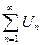 абсолютно сходится абсолютно сходится
| 1) 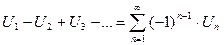
| 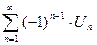 сходится сходится
| ||
2) 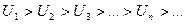
| Þ | 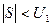
| ||
3) 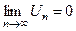
| 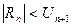
| |||
Замечание:
1. В сходящемся знакочередующемся ряде 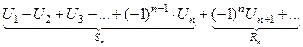 сумма S может быть заменена сумма S может быть заменена 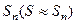 . Получаемая погрешность . Получаемая погрешность 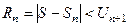 2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если
2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если 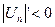 с некоторого номера, то члены ряда с некоторого номера, то члены ряда 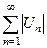 убывают с этого номера.
3. Если расходимость ряда убывают с этого номера.
3. Если расходимость ряда 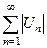 установлена признаком Даламбера или признаком Коши, то и ряд установлена признаком Даламбера или признаком Коши, то и ряд 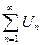 расходится, т. к. если расходится, т. к. если 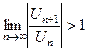 или или 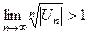 , то , то 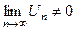 . .
| ||||
Алгоритм исследования знакопеременного ряда 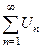 на сходимость. на сходимость.
| ||||
1. Составить ряд из абсолютных членов данного ряда 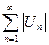 и исследовать его сходимость.
2. а) и исследовать его сходимость.
2. а) 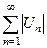 сходится сходится 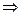 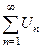 абсолютно сходится; б) абсолютно сходится; б) 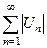 расходится расходится 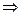 3 исследуй
3. Проверить условия признака Лейбница
Если 1) члены чередуются по знаку;
2) 3 исследуй
3. Проверить условия признака Лейбница
Если 1) члены чередуются по знаку;
2) 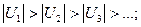 3)
3) 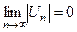 то 1) то 1) 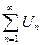 сходится по признаку Лейбница
2) сходится по признаку Лейбница
2) 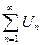 условно сходится, т. к. условно сходится, т. к. 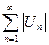 расходится расходится
| ||||
Знакопеременные числовые ряды
|
|

Сейчас читают про:
 2015-01-21
2015-01-21 639
639







