1.  Вычислить:
Вычислить: 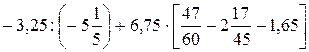 .
.
Решение. Указанные действия надо выполнить, не пользуясь микрокалькулятором, не делая округлений и приближенных вычислений, так как предполагается, что все заданные числа являются точными.
Будем выполнять вычисления по действиям:
1). 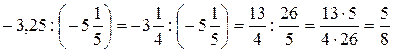 .
.
2). 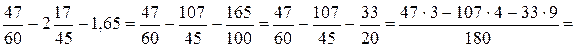
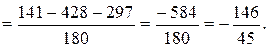
3). 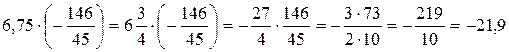 .
.
4). 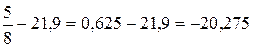 .
.
Таким образом, 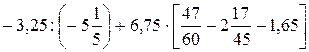 =
= 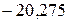 .
.
2. Упростить выражение: 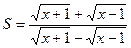 , при
, при 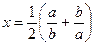 ,
, 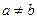 и
и 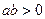 .
.
Решение. Покажем прежде, что при заданном условии все подкоренные выражения положительны:
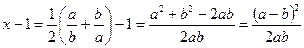 ,
,
поскольку 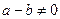 , то
, то 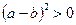 ;
; 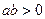 по условию.
по условию.
Следовательно, дробь 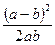 положительна, т.е.
положительна, т.е. 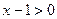 , а значит, и
, а значит, и 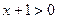 .
.
Теперь перейдем к упрощению заданного выражения. Освободимся от иррациональности в знаменателе:
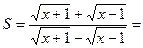
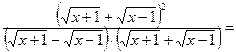
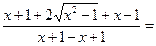
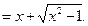
Подставляя значение 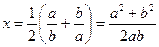 , получим
, получим
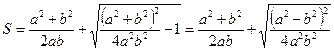
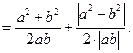
По условию 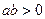 , значит,
, значит, 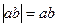 , поэтому
, поэтому 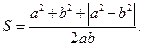
Рассмотрим оба возможных случая:
1) если 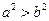 , т.е. если
, т.е. если 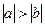 , то
, то 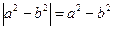 и
и 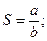
2) если 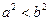 , т.е. если
, т.е. если 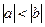 , то
, то 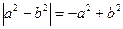 и
и 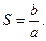
3. Сократить дробь: 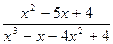 .
.
Решение. Разложим числитель и знаменатель на множители. Корни числителя: 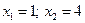 , поэтому, имеем:
, поэтому, имеем: 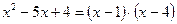 .
.
Чтобы разложить знаменатель на множители, применим метод группировки:
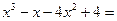
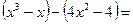
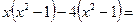
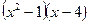 =
= 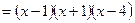 .
.
Тогда при 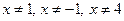 , будем иметь:
, будем иметь:
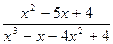 =
= 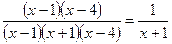 .
.
4. Пользуясь теоремой Виета, вычислить: 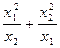 , где
, где 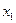 и
и 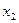 - корни уравнения
- корни уравнения 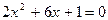 .
.
Решение. Преобразуем исходное выражение в дробь 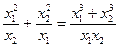 . Числитель данного выражения может быть разложен, как сумма кубов двух выражений:
. Числитель данного выражения может быть разложен, как сумма кубов двух выражений: 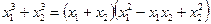 . Проведем тождественные преобразования:
. Проведем тождественные преобразования:
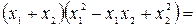
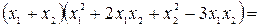
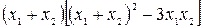
Воспользуемся теоремой Виета. Для начала убедимся, что дискриминант квадратного трехчлена 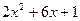 больше нуля.
больше нуля.
Действительно: 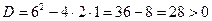 . Следовательно, у уравнения
. Следовательно, у уравнения 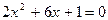 имеются два действительных корня, и теорема Виета может быть применена.
имеются два действительных корня, и теорема Виета может быть применена.
Таким образом, 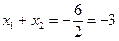 , и
, и 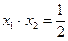 . Поэтому, имеем:
. Поэтому, имеем:
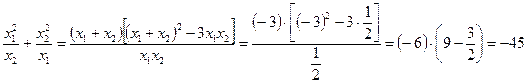 .
.
 2015-01-21
2015-01-21 1699
1699








